дЄАдЄ™еЕЙе≠¶з≥їзїЯзЪДиЃЊиЃ°пЉМжЧ†иЃЇжШѓжИРеГПеЕЙе≠¶з≥їзїЯињШжШѓйЭЮжИРеГПеЕЙе≠¶з≥їзїЯпЉМењЕй°їеМЕжЛђеЕЙе≠¶йХЬзїДгАБеЕЙжЇРгАБжО•жФґеЩ®дЄЙдЄ™йГ®еИЖгАВйАЪеЄЄеЕЙжЇРеИЖ䪯姩зДґеЕЙжЇРдЄОдЇЇеЈ•еЕЙжЇРпЉМ姙йШ≥жШѓеЬ∞зРГдЄКжЬАе§ІзЪД姩зДґеЕЙжЇРпЉМдЇЇз±їдљњзФ®еМЦе≠¶еПШеМЦпЉИзЗГзГІпЉЙгАБзЙ©зРЖеПШеМЦпЉИйАЪзФµ/еЬЇпЉЙз≠ЙеОЯзРЖдЇІзФЯзЪДеЕЙжЇРеИЩеЭЗе±ЮдЇОдЇЇеЈ•еЕЙжЇРгАВињСдЇФеНБеєіжЭ•дЇЇеЈ•еЕЙжЇРзЪДиЃЊиЃ°еИґйА†жЬЙзЭАйХњиґ≥зЪДињЫж≠•пЉМзФ±еОЯеІЛзЪДеМЦе≠¶иГљиљђеМЦдЄЇеЕЙиГљйАРжЄРж≠•еЕ•еИ©зФ®зФµиГљиљђеМЦдЄЇеЕЙиГљзЪДжЧґдї£гАВжЬђзѓЗжЦЗзЂ†еН≥еѓєAOIеЕЙе≠¶ж£АжµЛз≥їзїЯдЄ≠жЙАдљњзФ®еИ∞еЕЙжЇРзЪДз±їеЮЛгАБжАІиі®гАБеОЯзРЖгАБзЙєзВєињЫи°МељТзЇ≥жАїзїУгАВ
жЦЗзЂ†иЊГйХњпЉМиѓЈеЦДзФ®Ctrl+fж†єжНЃoutlineдЄЛеЕ≥йФЃе≠ЧеЬ®жЬђй°µйЭҐж£А糥пЉМжИЦжШѓдљњзФ®зЯ•дєОжЦ∞еҐЮзЪДзЫЃељХеКЯиГљпЉИињЩдЄ™еКЯиГљзЬЯй¶ЩпЉЙ
еЕ®жЦЗдЄ§дЄЗеЕЂеНГе≠ЧпЉМжЬЙдЄАзђФж≤°дЄАзђФзЪДеЖЩдЇЖдЄ§еєігАВ
Outline:
дЄАгАБеЕЙжЇРзЪДеЇ¶йЗП
- йїСдљУиЊРе∞Д
- ж≥ҐйХњ
- иЊРзЕІеКЯзОЗ/иЊРзЕІеЇ¶
- жµБжШО
- зЕІеЇ¶гАБеЕЙеЉЇгАБдЇЃеЇ¶дЄОеЕЙйАЪйЗП
- еЕЙеЉЇжµЛйЗПеЃЪеЊЛ
дЇМгАБеЕЙжЇРзІНз±ї
- еН§зі†зБѓ
- зЩљзВљзБѓ
- жЧ•еЕЙзБѓ
- ж∞ЩзБѓ
- LED
- жњАеЕЙ/йХ≠е∞Д
дЄЙгАБиЙ≤ељ©дЄОйҐСи∞±
- еК†иЙ≤жЈЈеРИдЄОеЗПиЙ≤жЈЈеРИ
- жЉФиЙ≤жАІжМЗжХ∞ Color Rendering Index, CRI
- еЖЈиЙ≤дЄОжЪЦиЙ≤
еЫЫгАБеЕЙжЇРдЄОжСДељ±жЬЇ
- жДЯеЕЙеЕГдїґзЪДеЕЙи∞±жХПжДЯеЇ¶
- зЩљеє≥и°°
дЇФгАБеЕЙжЇРдЄОеЊЕжµЛзЙ©
- жШОдЄОжЪЧ
- йШіељ±зЪДжЄРжЩХ
еЕ≠гАБеЕЙжЇРдЄОжї§еЕЙзЙЗ
- жї§еЕЙзЙЗзЪДеОЯзРЖ
- жї§еЕЙзЙЗзЪДйЩРеИґ
дЄГгАБеЕЙжЇРзЪД嚥еЉПдЄОйАЙжЛ©
a.еЙНзЕІеЉПFront Illumination
- зЫіеРСеЮЛеЙНеЕЙжЇРDirectional Front Lighting
- жЙ©жХ£еЮЛеЙНеЕЙжЇРDiffuse Front Lighting
- з΃嚥еЙНеЕЙжЇРRing Front Lighting
- дљОиІТеЇ¶еЙНеЕЙжЇРOblique Front Lighting
- еРМиљіеЙНеЕЙжЇРCoaxial Front Lighting
b.иГМзЕІеЉПBack Illumination
- зЫіеРСеЮЛиГМеЕЙжЇРDirection Back Lighting
- жЙ©жХ£еЮЛиГМеЕЙжЇРDiffuse Back Lighting
c.е§НеРИеЕЙжЇРHybrid light source
еЕЂгАБеЕЙе≠¶иљѓдїґдЄ≠зЪДеЕЙжЇРж®°жЛЯ
еРОиЃ∞
<hr/>дЄАгАБеЕЙжЇРзЪДеЇ¶йЗП
1.йїСдљУиЊРе∞Д
еЬ®еЕЙзЪДж≥ҐеК®жАІдЄОз≤Те≠РжАІзЪДдЇЙиЃЇдєЛеЙНпЉМдїОйТїжЬ®еПЦзБЂеЉАеІЛдЇЇз±їе∞±жДПиѓЖеИ∞еЕЙзЪДеЗЇзО∞йАЪеЄЄдЉЪдЉійЪПзЭАзГ≠иГљзЪДдЇ§жНҐгАВеЬ®е§ІиЛ±еНЪзЙ©й¶ЖзЪДй¶ЖиЧПдЄ≠жЬЙдЄАзЙЗеРНдЄЇе∞ЉеІЖй≤БеЊЈйАПйХЬпЉИNimrud lensпЉЙзЪДж∞іжЩґжЭРиі®жЩґзЙЗпЉМжШѓдЄАзЙЗе§ІзЇ¶еЬ®еЕђеЕГеЙНеЕЂдЄЦзЇ™зФ±дЇЪињ∞дЇЇеИґйА†пЉМ襀зЫЄеЕ≥з†Фз©ґдЇЇеСШиЃ§дЄЇеЕґдЄАзІНзФ®йАФзЪДеПѓиГљжАІдЄЇиБЪзĶ姙йШ≥еЕЙеПЦзБЂ[1]гАВ

еЫЊ1 the Nimrud lens in the british museum
иАМжЫізЫіжО•зЪДжЦЗе≠ЧиЃ∞иљљеПКжЦЗзЙ©иАГеП§еПСзО∞зЪДпЉМеИЩжШѓжЬАжЧ©еЗЇзО∞дЇОи•њеС®дЄ≠жЬЯзЪДйШ≥зЗІпЉИеПИзІ∞е§ЂзЗІпЉЙ[2]гАВгАКеС®з§Љ¬ЈзІЛеЃШеПЄеѓЗзђђдЇФгАЛиЃ∞иљљпЉЪвАЬеПЄзГЬпЉИhu«РпЉЙ[3]ж∞ПпЉМжОМдї•е§ЂзЗІеПЦжШОзБЂжЦЉжЧ•пЉМдї•йЙіеПЦжШОж∞іжЦЉжЬИпЉМдї•дЊЫз•≠з•АдєЛжШОйљНгАБжШОзГЫпЉМеЕ±жШОж∞ігАВвАЭињЩжЃµжЦЗе≠ЧиЃ∞иљљеС®жЬЭжЧґжЬЯиЃЊзЂЛзЪДеПЄзГЬж∞ПдЄАиБМпЉМиіЯиі£зФ®йШ≥зЗІеПЦеРСжЧ•жШОзБЂзВєзЗГз•≠з•АзФ®зЪДзБЂзГЫгАВ

еЫЊ2 йШ≥зЗІпЉМзФ®йЭТйУЬеЩ®йУЄйА†иАМжИРпЉМеК†дї•жЙУз£®еРО嚥жИРеЗєйЭҐйХЬ
еЬ®еЕЙ襀иѓБжШОжШѓдЄАзІНзФµз£БиЊРе∞ДдєЛеРОпЉМзФ®дЄАдЄ™зГ≠еКЫе≠¶ж®°еЮЛдљЬдЄЇеЃЪйЗПеЇ¶йЗПеЕЙзЪДеПВзЕІе∞±дЊњжИРдЄЇдЄАдЄ™йЭЮеЄЄеПѓйЭ†зЪДжЦєж≥ХгАВ1862еєіеЊЈеЫљзЙ©зРЖе≠¶еЃґеП§жЦѓе°Фе§Ђ¬ЈеЯЇе∞ФйЬНе§ЂжПРеЗЇйїСдљУпЉИBlack bodyпЉЙж¶ВењµпЉМеєґеЉХеЕ•зГ≠еКЫе≠¶еЖЕгАВ
йїСдљУжШѓдЄАдЄ™зРЖжГ≥еМЦзЪДзЙ©дљУпЉИObjectпЉЙ,еЃГиГље§ЯеРЄжФґе§ЦжЭ•зЪДеЕ®йГ®зФµз£БиЊРе∞ДпЉМеєґдЄФдЄНдЉЪжЬЙдїїдљХзЪДеПНе∞ДдЄОйАПе∞ДгАВйїСдљУеѓєдЇОдїїдљХж≥ҐйХњзЪДзФµз£Бж≥ҐзЪДеРЄжФґз≥їжХ∞дЄЇ1пЉМйАПе∞Дз≥їжХ∞дЄЇ0гАВйїСдљУжЬ™ењЕжШѓйїСиЙ≤зЪДпЉМеЃЪдєЙеЕґеРЄжФґз≥їжХ∞дЄЇ1пЉМеН≥дЄНеПНе∞ДдїїдљХзФµз£Бж≥ҐпЉМеЃГдїНзДґеПѓдї•еПСеЗЇзФµз£Бж≥ҐпЉМињЩдЇЫзФµз£Бж≥ҐзЪДйҐСи∞±еТМиГљйЗПеИЩеП™еПЦеЖ≥дЇОйїСдљУзЪДжЄ©еЇ¶пЉИзГ≠еКЫе≠¶жЄ©еЇ¶пЉМеНХдљНпЉЪеЉАе∞ФжЦЗпЉМKпЉЙпЉМдЄНеЫ†еЕґдїЦе§ЦзХМеЫ†зі†жФєеПШгАВ
姙йШ≥зЪДиЊРе∞ДзЙєжАІжШѓзЫЃеЙНеЈ≤зЯ•жЬАжО•ињСзРЖжГ≥йїСдљУзЪДзЙ©дљУпЉМ姙йШ≥дљЬдЄЇдЄАзІН姩зДґеЕЙжЇРпЉМжШѓдЄАдЄ™еЈ®е§ІдЄФйЂШжЄ©зЪДзФµжµЖдљУпЉМеЕЙи∞±иМГеЫізФ±зіЂе§ЦеЕЙиЗ≥ињЬзЇҐе§ЦеЕЙпЉМжАІиГљжО•ињСдЄАдЄ™еЃМзЊОзЪДйїСдљУиЊРе∞ДгАВињЩйЗМйЬАи¶БеЉЇи∞ГпЉМйїСдљУиЊРе∞ДжМЗе§ДдЇОзГ≠еКЫе≠¶еє≥и°°жАБзЪДйїСдљУеПСеЗЇзЪДзФµз£БиЊРе∞ДпЉМдЇІзФЯзЪДеЕЙи∞±жШѓињЮзї≠зЪДпЉМжШѓеЕЙеТМзЙ©иі®иЊЊеИ∞еє≥и°°жЙАи°®зО∞еЗЇзЪДзО∞и±°гАВжППињ∞еЕЙдЄОзЙ©иі®иЊЊеИ∞еє≥и°°жЧґеЕЙзЪДйҐСи∞±еИЖеЄГе∞±жШѓжЩЃжЬЧеЕЛеИЖеЄГпЉИPlanck distributionпЉЙпЉМе¶ВеЫЊ3жЙАз§ЇпЉМдЄНеРМзЪДжЄ©еЇ¶дЄЛйїСдљУиЊРе∞ДиГљйЗПпЉИSpectral energy densityпЉЙдЊЭж≥ҐйХњзЪДеИЖеЄГдїЕдЄОжЄ©еЇ¶жЬЙеЕ≥гАВ

еЫЊ3 жЩЃжЬЧеЕЛеИЖеЄГпЉИPlanck distributionпЉЙ
жППињ∞дїїжДПжЄ©еЇ¶дЄЛдЄАдЄ™йїСдљУдЄ≠еПСе∞ДеЗЇзЪДзФµз£БиЊРе∞ДзЪДиЊРе∞ДзОЗдЄОйҐСзОЗ/ж≥ҐйХњдєЛйЧізЪДеЕ≥з≥їпЉМеН≥дЄЇжЩЃжЬЧеЕЛеЃЪеЊЛпЉИPlanck&#39;s lawпЉЙпЉМиЊРе∞ДзОЗ I_{\lambda} дЄОж≥ҐйХњ \lambda гАБжЄ©еЇ¶ T дєЛйЧізЪДеЗљжХ∞еЕ≥з≥їдЄЇпЉЪ
I_{\lambda}(\lambda,T)=\frac{2hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda kT}}-1}\tag{1}
е∞Зж≥ҐйХњиљђжНҐдЄЇйҐСзОЗпЉМеИЩеЊЧеИ∞иЊРе∞ДзОЗ I_{\nu} дЄОйҐСзОЗ \nu жЄ©еЇ¶ T дєЛйЧізЪДеЗљжХ∞еЕ≥з≥їпЉЪI_{\nu}(\nu,T)=\frac{2h\nu^2}{c^2}\frac{1}{e^{\frac{h\nu}{kT}}-1}\tag{2} еЕґдЄ≠ I_{\lambda} жИЦ I_{\nu} жШѓиЊРе∞ДзОЗпЉМ \nu дЄЇзФµз£БиЊРе∞ДйҐСзОЗпЉМ \lambda дЄЇж≥ҐйХњпЉМ T дЄЇйїСдљУзїЭеѓєжЄ©еЇ¶пЉМ h=6.62607015√Ч10^{вИТ34}(J¬Јs) дЄЇжЩЃжЬЧеЕЛеЗљжХ∞пЉМ c=299792458m/s дЄЇеЕЙйАЯпЉМ k=1.380649√Ч10^{вИТ23}J/K дЄЇзОїе∞ФеЕєжЫЉеЄЄжХ∞гАВ
еЉПпЉИ1пЉЙдЄОеЉПпЉИ2пЉЙдЄ≠иЊРе∞ДзОЗ I_{\lambda} дЄО I_{\nu} еЕЈжЬЙдЄНеРМеНХдљНпЉЫ I_{\lambda} дЄЇеНХдљНж≥ҐйХњйЧійЪФеЖЕзЪДиЊРе∞ДзОЗпЉМ I_{\nu} дЄЇеНХдљНйҐСзОЗйЧійЪФеЖЕзЪДиЊРе∞ДзОЗпЉМеЫ†ж≠§дЇМиАЕдЄНз≠ЙдїЈпЉМйАЪињЗеЕЙйАЯдЄНеПШжЭ°дїґдЄЛгАБйҐСзОЗдЄОж≥ҐйХњдєЛйЧізЪДеЕ≥з≥їпЉМдЄ§дЄ™еЗљжХ∞е¶ВеЉПпЉИ3пЉЙжЙАз§ЇеПѓдї•зЫЄдЇТиљђжНҐгАВ
I_{\lambda}(\lambda,T)d\lambda=-I_{\nu}(\nu,T)d\nu\tag{3} е∞ЖеЉПпЉИ1пЉЙеѓєж≥ҐйХњињЫи°МзІѓеИЖпЉМеН≥еПѓеЊЧеИ∞еЬ®жЙАжЬЙж≥ҐйХњдЄЛзЪДиЊРе∞ДеКЯзОЗпЉМеЕґзїУжЮЬе∞±жШѓжЦѓзЙєжљШ-зОїе∞ФеЕєжЫЉеЃЪеЊЛпЉИStefan-Boltzmann lawпЉЙпЉЪW_{tot}=\sigma T^{4}\tag{4}еЕґдЄ≠ W_{tot} дЄЇеНХдљНйЭҐзІѓзЪДжАїиЊРе∞ДеКЯзОЗпЉИеНХдљНпЉЪзУ¶зЙєжѓПеє≥жЦєз±≥пЉМ W/m^2 пЉЙпЉМ T дЄЇйїСдљУзЪДзїЭеѓєжЄ©еЇ¶пЉИеНХдљНпЉЪеЉАе∞ФжЦЗпЉМ K пЉЙпЉМ \sigma=5.6704\times10^{-8}J\cdot s^{-1}\cdot m^{-2}\cdot K^{-4} дЄЇжЦѓзЙєжљШ-зОїе∞ФеЕєжЫЉеЄЄжХ∞гАВиѓ•еЃЪзРЖжМЗеЗЇпЉМдЄАдЄ™йїСдљУи°®йЭҐпЉМеНХдљНйЭҐзІѓгАБеНХдљНжЧґйЧіеЖЕйЗКжФЊеЗЇзЪДиГљйЗПж≠£жѓФдЇОеЕґзїЭеѓєжЄ©еЇ¶зЪДеЫЫжђ°жЦєгАВ
е∞ЖеЉПпЉИ1пЉЙеѓєж≥ҐйХњињЫи°МеЊЃеИЖпЉМдЄФдї§еЕґзїУжЮЬдЄЇйЫґпЉМеН≥еПѓж±ВеЊЧеЗљжХ∞жЮБзВєпЉМеЊЧеИ∞дљХзІНж≥ҐйХњ \lambda_{max} дЉЪдљњеЊЧ I_{\lambda} дЄЇжЬАе§ІеАЉгАВзїіжБ©дљНзІїеЃЪеЊЛпЉИWien&#39;s displacement lawпЉЙжППињ∞йїСдљУзФµз£БиЊРе∞ДеЕЙи∞±иЊРе∞ДзОЗ I_{\lambda} е≥∞еАЉж≥ҐйХњ \lambda_{max} дЄОйїСдљУзїЭеѓєжЄ©еЇ¶йЧіеПНжѓФдЊЛеЕ≥з≥їзЪДеЃЪеЊЛпЉЪ
\lambda_{max}=\frac{b}{T}=2.897 7729√Ч 10^{вАУ3}T^{-1}m\tag{5} еЬ®ж≥ҐйХњ \lambda_{max} дЄЛиЊРе∞ДзОЗ I_{\lambda} е≥∞еАЉдЄЇпЉЪ
I_{\lambda,max}=1.286\times10^{-5}T^{5} W/m^{2}\cdot m^{-1}\tag{6} дї•дЄКдЊњжШѓжЩЃжЬЧеЕЛеИЖеЄГдЄ≠еРДй°єзЙєеЊБеАЉзЪДиЃ°зЃЧпЉМжИСдїђдї•е§ЬиІЖз≥їзїЯдЄЇдЊЛжППињ∞жЩЃжЬЧеЕЛеИЖеЄГеЬ®еЃЮйЩЕеЈ•з®ЛдЄ≠зЪДеЇФзФ®пЉЪ
EXAMPLEпЉЪдЄАдЄ™дљНдЇО27¬∞CпЉИзїЭеѓєжЄ©еЇ¶300KпЉЙзЪДйїСдљУпЉМеЕґжАїеПСе∞ДиЊРе∞ДдЄЇпЉЪW_{tot}=5.67\times10^{-12}(300)^{4}=4.59\times10^{-12}W/cm^{2}\\жЬАе§І I_{\lambda} е≥∞еАЉж≥ҐйХњ \lambda_{max} дЄЇпЉЪ\lambda_{max}=\frac{b}{T}=2.897 7729√Ч 10^{вАУ3}(300)^{-1}m=9.66\mu m\\ еПѓеЊЧжЬАе§І I_{\lambda} е≥∞еАЉпЉЪI_{\lambda,max}=1.286\times10^{-5}(300)^{5} =3.13\times10^{7}W/m^{2}\cdot m^{-1}\\ дЇОжШѓжИСдїђеЊЧеИ∞зїУиЃЇпЉЪеЬ®ж≥ҐйХњ 10\mu m зЪДж≥ҐжЃµжЙАжЬЙдЇЛзЙ©зЪЖжЬЙжЬАеЉЇзЪДеПСе∞ДиЊРе∞ДпЉМе§ЬиІЖдї™зЪДжДЯжµЛжЩґзЙЗйЬАи¶БйТИеѓєж≠§ж≥ҐжЃµињЫи°МиЃЊиЃ°гАВ
е§ІйГ®еИЖзГ≠иЊРе∞ДиЃ°дЄНжШѓзїЭеѓєйїСдљУпЉМжЧ†ж≥ХеБЪеИ∞еЃМеЕ®дЄНеПНе∞ДжИЦйАПе∞Де§ЦжЭ•зЪДзФµз£БиЊРе∞ДпЉМеЫ†ж≠§ињЩж†ЈзЪДзЙ©дљУзІ∞дєЛдЄЇзБ∞дљУпЉИGray-bodiesпЉЙжЫідЄЇиііеИЗгАВзБ∞дљУдЄОйїСдљУжАІиі®з±їдЉЉпЉМеЬ®зЫЄеРМзЪДжЄ©еЇ¶дЄЛжЬЙзЭАеРМж†ЈзЪДеЕЙи∞±зЙєжАІељ±еГПпЉМеП™жШѓеЕґеЫ†еПЧеИ∞еПНе∞ДжИЦйАПе∞Де§ЦжЭ•зФµз£БиЊРе∞ДзЪДељ±еУНиАМеЉЇеЇ¶з®НдљОгАВж≠§е§ДеЉХеЕ•жАїеПСе∞Дз≥їжХ∞/жАїеПСе∞ДзОЗпЉИTotal emissivity, \varepsilon пЉЙзЪДж¶ВењµпЉМеЬ®зЫЄеРМзЪДзїЭеѓєжЄ©еЇ¶дЄЛпЉЪ\varepsilon=\frac{зБ∞дљУжАїеПСе∞ДиЊРе∞Д}{зїЭеѓєйїСдљУжАїеПСе∞ДиЊРе∞Д}\tag{7} зїЭеѓєйїСдљУзЪД \varepsilon=1 гАВеЄЄиІБзЙ©иі®зЪДжАїеПСе∞Дз≥їжХ∞е¶ВдЄЛжЦєйУЊжО•жЙАз§ЇпЉМйЬАж≥®жДПжАїеПСе∞Дз≥їжХ∞жШѓдЉЪйЪПзЭАж≥ҐйХњеТМжЄ©еЇ¶иАМеПШеК®зЪДгАВ
еѓєдЇОдЄАзЙ©дљУзЪДе§ЦйГ®иЊРе∞ДпЉМиѓ•зЙ©дљУжШѓеσ俕襀穜йАПгАБеПНе∞ДпЉИжХ£е∞ДпЉЙжИЦиАЕеРЄжФґзЪДпЉМз©њйАПзОЗгАБеПНе∞ДзОЗгАБеРЄжФґзОЗжЬАе§ІеАЉзЪЖдЄЇ100%гАВеПСе∞ДзОЗзФ±з©њйАПзОЗеК†еПНе∞ДзОЗжЮДжИРпЉМеПСе∞ДзОЗдЄОеРЄжФґзОЗдЇТи°•дЄЇ100%гАВеЫ†ж≠§ељУдЄАдЄ™зЙ©дљУжЬЙзЭАйЂШз©њйАПзОЗжИЦиАЕйЂШеПНе∞ДзОЗпЉМдєЯењЕеЃЪжЬЙзЭАдљОеПСе∞Дз≥їжХ∞гАВ
ељУеЬ®е§ДзРЖзБ∞дљУйЧЃйҐШжЧґпЉМењЕй°їи¶Бе∞ЖеПСе∞Дз≥їжХ∞ \varepsilon дєШеЕ•йїСдљУеЕђеЉПпЉМжЩЃжЬЧеЕЛеЃЪеЊЛпЉИеЉПпЉИ1пЉЙпЉЙгАБжЦѓзЙєжљШ-зОїе∞ФеЕєжЫЉеЃЪеЊЛпЉИеЉПпЉИ4пЉЙпЉЙгАБзїіжБ©дљНзІїеЃЪеЊЛпЉИеЉПпЉИ6пЉЙпЉЙзЪЖжШѓе¶Вж≠§гАВеѓєе§ІйГ®еИЖзЙ©иі®жЭ•иѓіеПСе∞Дз≥їжХ∞йГљжШѓж≥ҐйХњзЪДеЗљжХ∞пЉМдЊЛе¶ВзОїзТГпЉМеЬ®жЯРдЇЫж≥ҐйХњдєЛдЄЛжЬЙзЭАеПѓдї•ењљзХ•зЪДеРЄжФґзОЗдЄОдљОеПСе∞ДзОЗпЉМдљЖжШѓеЬ®еЕґдїЦж≥ҐйХњдєЛдЄЛеИЩдЉЪеЃМеЕ®еРЄжФґгАВж≠§жГЕ嚥胕зЙ©иі®зЪДеПСе∞Дз≥їжХ∞е∞±дЉЪеПШдЄЇеЕ≥дЇОеЕЙи∞±зЪДеЗљжХ∞пЉМжИРдЄЇеЕЙи∞±еПСе∞Дз≥їжХ∞гАВйЬАж≥®жДПжЬЙдЇЫеЕЙжЇРзЪДеЕЙи∞±дЄНжШѓињЮзї≠зЪДпЉМеЫ†ж≠§еЕЙи∞±еПСе∞Дз≥їжХ∞еЗљжХ∞дЄНдЄАеЃЪжШѓињЮзї≠еЗљжХ∞гАВйАЪеЄЄе§Іе§ЪжХ∞зЙ©иі®ж≥ҐйХњиґКйХњеЕґеПСе∞Дз≥їжХ∞иґКе∞ПпЉМжЄ©еЇ¶иґКйЂШеЕґеПСе∞Дз≥їжХ∞иґКе§ІгАВ
дї•дЄКеЕ≥дЇОйїСдљУзЪДдїЛзїНжШОз°ЃдЇЖйїСдљУжЄ©еЇ¶гАБж≥ҐйХњи∞±/йҐСи∞±йЧізЪДеЕ≥з≥їпЉМеЫ†ж≠§жИСдїђеПѓдї•еЉХеЕ•иЙ≤жЄ©пЉИColor temperatureпЉЙзЪДж¶ВењµжЭ•еЃЪдєЙеЕЙжЇРзЪДйҐЬиЙ≤гАВ
еЕЙжЇРзЪДиЙ≤жЄ©еЃЪдєЙдЄЇдЄОж≠§еЕЙжЇРеПСеЗЇзЫЄдЉЉеЕЙзЪДйїСдљУиЊРе∞ДжЙАеЕЈжЬЙзЪДеЉАе∞ФжЦЗжЄ©еЇ¶гАВ
дїОеЫЊ3жЩЃжЬЧеЕЛеИЖеЄГжИСдїђеПѓдї•зЬЛеЗЇпЉМеѓєдЇОдЄАдЄ™жЮБдЇЃдЄОжЮБжЪЧзЪДеЕЙжЇРпЉМиЛ•жШѓдЊЭжНЃеЕґж≥ҐйХњгАБеЉЇеЇ¶пЉМиРљеЬ®зЫЄеРМзЪДжЄ©еЇ¶жЫ≤зЇњдЄКпЉМеЕґдїНзДґеЕЈжЬЙзЫЄеРМзЪДиЙ≤жЄ©гАВеѓєдЇОеРМдЄАж≥ҐйХњзЪДеЕЙжЇРпЉМеЕґеЉЇеЇ¶жИЦиЊРе∞ДеКЯзОЗдЄНеРМе∞±жДПеС≥зЭАеЉЇеЇ¶/иЊРе∞ДеКЯзОЗиґКеЉЇпЉМиЙ≤жЄ©иґКйЂШгАВиЙ≤жЄ©еѓєдЇОиЙ≤ељ©зЪДиІ£жЮРжШѓеНБеИЖйЗНи¶БзЪДгАВ
еЃЮйЩЕеЇФзФ®дЄ≠еП™жЬЙељУеЕЙжЇРеПСеЗЇзЪДеЕЙеТМйїСдљУиЊРе∞ДзЪДеЕЙз±їдЉЉжЧґпЉИеЕЙи∞±иМГеЫіз±їдЉЉпЉЙпЉМиЙ≤жЄ©жЙНжЬЙеЃЪдєЙгАВеЬ®дЄНеРМиЙ≤жЄ©дЄЛпЉМеЕЙи∞±зїЉеРИи°®зО∞еЗЇзЪДиЙ≤ељ©жДЯиІЙпЉИе§ІйҐСеЃљзЪДйҐСи∞±жЮДжИРзЪДеЕЙињСдЉЉдЇОзЩљеЕЙпЉЙжОТеИЧе¶ВеЫЊ4жЙАз§ЇпЉМзФ±дЇОиЙ≤жЄ©дЄНеРМгАБйҐСи∞±дЄКеЉЇеЇ¶еАЉжЬАе§ІгАБжЙАеН†жЭГйЗНжЬАе§ІзЪДж≥ҐйХњдєЯдЄНеРМпЉМиЙ≤жЄ©зФ±дљОеИ∞йЂШеИЖеИЂзїЩдЇЇзЬЉжДЯзЯ•еСИзО∞еЗЇзЇҐ-ж©Щ-йїД-зЩљ-жµЕиУЭињЩдЇЫйҐЬиЙ≤гАВељУиЃ®иЃЇиЙ≤жЄ©жЧґпЉМиЃ®иЃЇеЕЈдљУжЯРзІНж≥ҐйХњзЪДйҐЬиЙ≤дЊЛе¶ВзїњиЙ≤гАБзіЂиЙ≤иЙ≤жЄ©жЧґж≤°жЬЙжДПдєЙзЪДпЉМеЫ†дЄЇињЩдЇЫйҐЬиЙ≤йГљеП™еН†жНЃйїСдљУиЊРе∞ДеЕЙи∞±зЪДйГ®еИЖйҐСзОЗиАМйЭЮжХідЄ™йїСдљУиЊРе∞ДеЕЙи∞±гАВ

еЫЊ4 800K-12200KзЪДйїСдљУиЊРе∞ДеЕЙи∞±
2.йҐЬиЙ≤еЃЪдєЙдЄОж≥ҐйХњ
жИСдїђиАГиЩСеПѓиІБеЕЙзЪДзФµз£БиЊРе∞ДпЉМеєґдЊЭзЕІж≥ҐйХњжОТеИЧеЗЇе¶ВеЫЊ5жЙАз§ЇзЪДеПѓиІБеЕЙеЕЙи∞±пЉИVisible Light SpectrumпЉЙпЉЪ

еЫЊ5 Visible Light Spectrum
еПѓиІБеЕЙеЕЙи∞±жґµзЫЦдЇЖдЇЇзЬЉеПѓдї•жДЯзЯ•зЪДеПѓиІБеЕЙж≥ҐйХњиМГеЫіпЉЪзЇ¶400nm~700nmгАВзДґиАМиІВеѓЯињЩдЄ™еПѓиІБеЕЙеЕЙи∞±дЄ≠еРДдЄ™ж≥ҐйХњзЪДеЕЙеЬ®дЇЇз±їиІЖиІЙжДЯзЯ•дЄЛзЪДйҐЬиЙ≤пЉМжИСдїђеПѓдї•еПСзО∞пЉЪеЊИе§ЪжИСдїђдЇЇзЬЉеПѓдї•жДЯзЯ•еИ∞зЪДйҐЬиЙ≤пЉМеєґдЄНе≠ШеЬ®дЇОеПѓиІБеЕЙеЕЙи∞±дЄ≠пЉМжѓФе¶ВпЉЪз≤ЙиЙ≤пЉИеЫЊ6пЉЙпЉЪ

еЫЊ6 з≤ЙиЙ≤
ињЩжШѓзФ±дЇОдЇЇз±їзЬЉзЭЫдЄ≠е≠ШеЬ®еЫЫзІНеЕЙжДЯеПЧеЩ®пЉМеМЕжЛђиГље§ЯдЊ¶жµЛйХњж≥ҐйХњпЉИLпЉМ560-580nmпЉЙгАБдЄ≠ж≥ҐйХњпЉИMпЉМ530-540nmпЉЙдЄОзЯ≠ж≥ҐйХњпЉИSпЉМ420-440nmпЉЙзЪДиІЖйФ•зїЖиГЮпЉМдї•еПКеНХдЄАиЙ≤пЉИ490-495nmпЉЙзЪДиІЖжЭЖзїЖиГЮпЉИжЫіе§ЪеЬ®жЪЧиІЖиІЙдЄ≠еПСжМ•дљЬзФ®пЉЙгАВељУиАГиЩСеИ∞дЇЇиГље§ЯжДЯеПЧеИ∞зЪДйҐЬиЙ≤жЧґпЉМжШЊзДґзФ®зФµз£Бж≥ҐеЕЙи∞±жЧ†ж≥ХеЃМжХіжППињ∞дЇЇиГље§ЯжДЯеПЧеИ∞зЪДжЙАжЬЙйҐЬиЙ≤пЉМиАМеѓєдЇОињЮзї≠ж≥ҐйХњеПШеМЦзЪДзФµз£Бж≥Ґи∞±иАМи®Адї•жОТеИЧзїДеРИзЪД嚥еЉПжППињ∞йҐЬиЙ≤жШЊзДґдЄНзО∞еЃЮпЉИеѓєдЇОдЄЙдЄ™еПКдї•дЄКж≥ҐйХњжЮДжИРзЪДеЕЙпЉМе∞ЖдЉЪиѓЮзФЯжЧ†жХ∞дЄ™зїДеРИжЦєеЉПпЉЙпЉМдЇОжШѓеЬ®йҐЬиЙ≤жДЯзЯ•зЪДз†Фз©ґдЄ≠пЉМж†єжНЃдЄЙзІНиІЖйФ•зїЖиГЮзЪДеИЇжњАжѓФдЊЛжППињ∞дїїдЄАзІНйҐЬиЙ≤зЪДжДЯиІЙпЉМзІ∞дєЛдЄЇLMSиЙ≤ељ©з©ЇйЧігАВ
зФ®дЇЇзЪДжДЯиІЙжЭ•зЫіжО•еЃЪдєЙйҐЬиЙ≤е∞±е•љеГПзФ®ж≥ХиАБе∞ПиЗВйХњеЇ¶жЭ•еЃЪдєЙе∞ЇдЄА憣姙ињЗдЇОзЙЗйЭҐпЉМеЫ†ж≠§йЬАи¶БеЬ®еЯЇдЇОдЇЇз±їжДЯзЯ•иЙ≤ељ©зЪДеОЯзРЖдєЛдЄКзФ®дЄАзІНжХ∞е≠¶жЦєж≥ХдљЬдЄЇеЃЪдєЙйҐЬиЙ≤зЪДеЈ•еЕЈгАВ1920еєідї£W. David WrightеТМJohn GuildдЄ§дЄ™дЇЇеРДиЗ™жЙЊдЇЖиЛ•еє≤иІВеѓЯиАЕпЉИobserversпЉЙињЫи°МдЇЖ写зІ∞дЇЇз±їзІСе≠¶еП≤жЬАе§НжЭВзЪДжОІеИґеПШйЗПж≥ХеЃЮй™МпЉМж±ЗйЫЖжИРдЄЇCIE1931 RGBйҐЬиЙ≤еМєйЕНеЗљжХ∞пЉИColor-matching functionsпЉЙпЉМе¶ВеЫЊ7жЙАз§ЇпЉЪ

еЫЊ7 Color-matching functions
йЬАи¶Бз®НеЊЃиІ£йЗКдЄАдЄЛињЩеєЕеЫЊжЙНиГљзРЖиІ£йҐЬиЙ≤еМєйЕНеЗљжХ∞жОІеИґдЇЖеУ™дЇЫеПШйЗПпЉМеУ™дЇЫжШѓиЗ™еПШйЗПгАБеУ™дЇЫжШѓеЫ†еПШйЗПгАВй¶ЦеЕИињЩдЄ™еЃЮй™МдЄ≠йАЙжЛ©зЪДдЄЙзІНеНХиЙ≤пЉЪ700 nmпЉИзЇҐиЙ≤пЉЙгАБ546.1 nmпЉИзїњиЙ≤пЉЙеТМ435.8 nmпЉИиУЭиЙ≤пЉЙзЪДдЄЙзІНеНХиЙ≤еЕЙжЇРпЉМзДґеРОдї•ињЩдЄЙзІНеНХиЙ≤еЕЙжЇРзЪДеЉЇеЇ¶дљЬдЄЇеПШйЗПпЉМдї• \bar{r}(\lambda) гАБ \bar{g}(\lambda) гАБ \bar{b}(\lambda) и°®з§ЇиІВжµЛиАЕпЉИObserverпЉЙиІЖиІЙдЄ≠жДЯеПЧеИ∞зЪДдЄЙиЙ≤еЉЇеЇ¶пЉИиѓ•еЉЇеЇ¶еАЉдЄЇе§ЪдЄ™еПЧиѓХиІВжµЛиАЕзЪДеє≥еЭЗеАЉпЉЙгАВзФ®дЄНеРМеЉЇеЇ¶зЪДињЩдЄЙзІНеНХиЙ≤еЗСеЗЇиІВжµЛиАЕиІЖиІЙдЄ≠з≠ЙжХИзЪДгАБињЮзї≠еЕЙи∞±дЄ≠еРДеНХдЄАж≥ҐйХњеЕЙзЪДйҐЬиЙ≤ C(\lambda) пЉМиОЈеЊЧињЮзї≠еПѓиІБеЕЙи∞±дЄКдЄНеРМж≥ҐйХњзЪДеНХиЙ≤еЕЙеПѓдї•зФ±дїАдєИж†ЈжѓФдЊЛзЪДдЄЙзІНеНХиЙ≤еЕЙжЮДжИРзЫЄеРМзЪДйҐЬиЙ≤пЉМе¶ВеЫЊ7жЙАз§ЇињЩдЄЙзІНеНХиЙ≤еЕЙељТдЄАеМЦеРОзЪДеЉЇеЇ¶жЫ≤зЇње∞±жШѓйҐЬиЙ≤еМєйЕНеЗљжХ∞пЉМеЕ≥з≥їеЉПдЄЇпЉЪ
C(\lambda)=\bar{r}(\lambda)+\bar{g}(\lambda)+\bar{b}(\lambda)\tag{8}
иѓ¶зїЖеЃЮй™МињЗз®ЛиѓЈеПВиАГпЉЪ
дЄЇдїАдєИдЉЪйАЙжЛ©700 nmгАБ546.1 nmеТМ435.8 nmињЩдЄЙзІНеНХиЙ≤еЕЙжЇРпЉЯињЩдєЯжШѓCIE1931жПРеЗЇињЗз®ЛдЄ≠жЬАдЄїи¶БзЪДдЇЙиЃЃзВєдєЛдЄАгАВињЩж†ЈзЪДж≥ҐйХњйАЙжЛ©зЫіжО•еѓЉиЗізЇҐиЙ≤ \bar{r}(\lambda) жЫ≤зЇњдЄНеПѓйБњеЕНзЪДе≠ШеЬ®иіЯеАЉпЉИињЩдЄАеМЇжЃµзФ±дЇОдЄЙзІНеНХиЙ≤жЧ†иЃЇжАОж†ЈйГљжЧ†ж≥ХеЗСеЗЇзЫЄеЇФзЪДеНХж≥ҐйХњйҐЬиЙ≤пЉМдЇОжШѓзФ®еЕґдЄ≠дЄ§зІНйҐЬиЙ≤пЉМ546.1 nmпЉИзїњиЙ≤пЉЙеТМ435.8 nmпЉИиУЭиЙ≤пЉЙпЉМжЈЈжИРеТМзЫЄеЇФеНХж≥ҐйХњеЕЙдЄО700 nmпЉИзЇҐиЙ≤пЉЙеЕЙжЈЈеРИзЪДеЕЙдЄАж†ЈзЪДйҐЬиЙ≤пЉМињЩж†ЈдЄАж†ЈдЄ§иЊєз≠ЙеЉПзЫЄз≠ЙпЉМе∞Ж700 nmеЕЙзЪДељТдЄАеМЦеЉЇеЇ¶зІїй°єеИ∞еП¶дЄАиЊєпЉМдЇОжШѓе∞±еЊЧеИ∞дЄАдЄ™жХ∞е≠¶дЄКзЪДиіЯеАЉпЉЙпЉМељУжЧґжЙАжЬЙCIEзЪДзЊОеЫљдЇЇжИРеСШйГљиЃ§дЄЇеЬ®еХЖдЄЪеТМеЈ•дЄЪдЄ≠дљњзФ®зЪДйҐЬиЙ≤йЗПжµЛз≥їзїЯдЄ≠ињЩж†ЈзЪДеЃЪдєЙдЄНеПѓжО•еПЧгАВињЩдЄЙдЄ™ж≥ҐйХњжШѓзФ±John GuildзЪДеЃЮй™МдЄ≠еЃЪдєЙзЪДпЉИW. David WrightеТМJohn GuildдЄ§дЄ™дЇЇеЭЗжЬЙеРДиЗ™еЃЪдєЙзЪДдЄЙзІНеОЯиЙ≤пЉЙпЉМдїЦиЃ§дЄЇеЕ≥дЇОж†ЗеЗЖжЛЯеЃЪзЪДеЯЇжЬђеУ≤е≠¶пЉМеЇФиѓ•жШѓжШОз°ЃзЪДгАБеЬ®зЙ©зРЖдЄКеПѓдї•з°ЃеЃЪеЃЮзО∞зЪДгАВ700nmжШѓеЕЙи∞±зЪДзЇҐиЙ≤зЂѓж≥ҐйХњпЉМеЕґйЩДињСж≥ҐжЃµйҐЬиЙ≤иЙ≤и∞ГеПШеМЦеЊИе∞ПпЉМиАМ546.1 nmеТМ435.8 nmжШѓж±ЮеЕЙи∞±дЄ≠жЬАжШОжШЊзЪДзїњиЙ≤зЇњдЄОзіЂиЙ≤зЇњ[4][5]гАВ

еЫЊ8 ж£±йХЬеИЖеЕЙиЃ°иІВжµЛзЪДж±ЮеЕЙи∞±
дЄЙиЙ≤еИЇжњАеАЉзФ±йҐСи∞±еКЯзОЗеИЖеЄГеЃЪдєЙпЉМдЄОйҐЬиЙ≤еМєйЕНеЗљжХ∞йЧіе≠ШеЬ®ињЩж†ЈзЪДзІѓеИЖеЕ≥з≥їпЉЪ
R=\int_{780nm}^{380nm}{\bar{r}P(\lambda)d\lambda}\\ G=\int_{780nm}^{380nm}{\bar{g}P(\lambda)d\lambda}\\ B=\int_{780nm}^{380nm}{\bar{b}P(\lambda)d\lambda}\tag{9} еЕґдЄ≠ P(\lambda) дЄЇзЫЄеѓєеЕЙи∞±еКЯзОЗеИЖеЄГеЗљжХ∞пЉМжЬАзїИиОЈеЊЧзЪДдЄЙиЙ≤еИЇжњАеАЉ R гАБ G гАБ B дЄЇеРДеНХиЙ≤еЕЙжЇРеЬ®еПѓиІБеЕЙж≥ҐжЃµгАБдЇЇзЬЉдЇІзФЯйҐЬиЙ≤жДЯиІЙзЪДеЕЙи∞±иГљйЗПгАВ
пЉИеЃЮй™МдЄ≠дЄЙиЙ≤еИЇжњАеАЉеЭЗеПѓзЫіжО•зФ±CIEж†ЗеЗЖиІВжµЛиАЕжµЛиѓХеЊЧзЯ•пЉМеЉХеЕ•иѓ•зїДзІѓеИЖеЉПжЭ•жППињ∞дЄЙиЙ≤еИЇжњАеАЉпЉМдЄ™дЇЇиІВзВєжШѓпЉЪзФ±дЇОеЃЮйЩЕдЄ≠еєґдЄНе≠ШеЬ®зїЭеѓєжДПдєЙзЪДеНХж≥ҐйХњеЕЙжЇРпЉМзФ±дЇОеЕЙжЇРзГ≠еКЫе≠¶зЙєжАІгАБзОѓеҐГжМѓеК®еѓЉиЗізЇҐзІїиУЭзІїз≠ЙзО∞и±°пЉМеЕЙжЇРеЭЗе≠ШеЬ®еЄ¶еЃљ/йҐСеЃљпЉМеЫ†ж≠§еЬ®зФ®жХ∞е≠¶и°®иЊЊеЉПжППињ∞ињЩдЄАеЃЮй™МеАЉжЧґпЉМењЕй°їи¶БиАГиЩСеИЇжњАеАЉжШѓзФ±вАЬеНХиЙ≤еЕЙжЇРвАЭеЕЙи∞±еКЯзОЗеИЖеЄГйА†жИРиАМйЭЮзРЖжГ≥еНХдЄАж≥ҐйХњгАВпЉЙ
зФ±дЇОзЇҐиЙ≤ \bar{r}(\lambda) жЫ≤зЇњдЄНеПѓйБњеЕНзЪДе≠ШеЬ®иіЯеАЉпЉМеЫ†ж≠§йЬАи¶БеѓєдЄЙиЙ≤еИЇжњАеАЉињЫи°МеРИйАВзЪДиљђжНҐпЉМиОЈеЊЧдЄЙдЄ™еТМдЄЙиЙ≤еИЇжњАеАЉжЬЙеЕ≥зЪДеПВжХ∞пЉМдЄФињЩдЄ™еПВжХ∞ењЕй°їйГљжШѓж≠£еАЉпЉМдї•дЊњеЬ®еЭРж†Зз≥їзЪДдЄАдЄ™и±°йЩРеЖЕи°®з§ЇйҐЬиЙ≤гАВдЇОжШѓйТИеѓє\bar{r}(\lambda) гАБ \bar{g}(\lambda) гАБ \bar{b}(\lambda) дЄЙдЄ™еЗљжХ∞зЪДдЄЙиЙ≤еИЇжњАеАЉ R гАБ G гАБ B пЉМеПѓдї•йАЪињЗзЯ©йШµиљђжНҐдЄЇ X гАБ Y гАБ Z еИЇжњАеАЉпЉЪ
\begin{vmatrix} X\\ Y\\ Z \end{vmatrix} = \begin{vmatrix} 2.768892 & 1.751748 & 1.130160 \\ 1.000000 & 4.590700 & 0.060100 \\ 0 & 0.056508 & 5.594292 \\ \end{vmatrix} \bullet \begin{vmatrix} R \\ G \\ B \end{vmatrix}\tag{10}ињЩдЄ™иљђжНҐзЯ©йШµзЪДеЕГзі†жХ∞еАЉзФ±CIE1931еЃЪдєЙгАВеРМж†ЈйАЪињЗињЩдЄ™зЯ©йШµеПШжНҐпЉМжИСдїђеПѓдї•е∞Ж \bar{r}(\lambda) гАБ \bar{g}(\lambda) гАБ \bar{b}(\lambda) дЄЙдЄ™еЗљжХ∞иљђжНҐдЄЇ\bar{x}(\lambda) гАБ \bar{y}(\lambda) гАБ \bar{z}(\lambda) дЄЙдЄ™еЗљжХ∞пЉМиОЈеЊЧCIE1931 XYZ йҐЬиЙ≤еМєйЕНеЗљжХ∞пЉИCIE 1931 XYZ Color Matching FunctionsпЉЙ[6]пЉЪ

еЫЊ9 CIE 1931 XYZ Color Matching Functions
зФ±дЇОдЄЙиЙ≤еИЇжњАеАЉжАїйЗПз°ЃеЃЪзЪДжГЕеЖµдЄЛпЉМеЈ≤зЯ•дЄ§зІНйҐЬиЙ≤зЪДеИЇжњАеАЉе∞±еПѓдї•з°ЃеЃЪиѓ•зІНйҐЬиЙ≤зЪДиЙ≤еЇ¶пЉМеЫ†ж≠§еПѓдї•зФ® x гАБ y дЄ§дЄ™еПШйЗПеЬ®дЇМзїіеЭРж†Зз≥їдЄ≠жППињ∞иЙ≤еЇ¶пЉМеН≥иЙ≤еЇ¶еЭРж†ЗпЉИChromaticity coordinatesпЉЙпЉМx гАБ y и°®з§ЇдЄЇпЉЪ
y=\frac{Y}{X+Y+Z}\tag{12}x=\frac{X}{X+Y+Z}\tag{13} Z еПѓдї•йАЪињЗ x гАБ y еАЉзФ® z еАЉжЭ•з°ЃеЃЪпЉЪ
z=\frac{Z}{X+Y+Z}=1-x-y\tag{14} еЬ®зЫіиІТеЭРж†Зз≥їдЄ≠зїШеЗЇx гАБ y пЉМе∞±жШѓCIE 1031 иЙ≤еЯЯз©ЇйЧіиЙ≤еЇ¶еЫЊпЉЪ

еЫЊ10 The CIE 1931 color space chromaticity diagram
жЬђжЦЗдЄНжЙУзЃЧе±ХеЉАзїЖињ∞иЙ≤ељ©з©ЇйЧіеПКжѓФиЙ≤ж≥ХпЉИColorimetryпЉЙеЬ®CIE1931иЙ≤еЯЯз©ЇйЧіжПРеЗЇдєЛеРОеБЪеЗЇзЪДзїЖиКВжФєињЫпЉИеЊИе§ІеОЯеЫ†жШѓжЬђдЇЇеЬ®ињЩдЄАйҐЖеЯЯзЪДзЯ•иѓЖеВ®е§ЗдЄНе§ЪпЉЙпЉМеЬ®иЗ™еК®еМЦеЕЙе≠¶ж£АжµЛйҐЖеЯЯзЪДељ±еГПеРОе§ДзРЖйШґжЃµпЉМељ±еГПиѓЖеИЂжЧґеБЪRGBйШИеАЉиЃЊеЃЪжШѓжѓФиЙ≤ж≥ХеЬ®ж≠§йҐЖеЯЯдЄЇжХ∞дЄНе§ЪзЪДеЇФзФ®дєЛдЄАгАВзДґиАМе∞±жИСзЪДзїПй™МиАМи®АпЉМжЬЙдЇЫеИЭе≠¶иАЕе≠¶еИ∞ињЩдЄАеЭЧзЯ•иѓЖеРОзЪДзїУжЮЬеЊАеЊАжШѓзБЊйЪЊжАІзЪДпЉЪжѓПеєіжАїжЬЙйВ£дєИеdž䪙姩жЙНе≠¶еЉЯжГ≥еИ∞пЉМдЄЇдїАдєИдЄНдїОRGBдЄКеБЪйҐЬиЙ≤жї§ж≥ҐпЉМињЩж†Је∞±дЄНзФ®еЬ®з≥їзїЯдЄ≠жЈїеК†жї§ж≥ҐзЙЗпЉМињШеПѓдї•зБµжіїйАЙжЛ©жї§ж≥Ґж≥ҐжЃµ......жЙАдї•еЬ®ињЩйЗМйЬАи¶БеЉЇи∞ГпЉЪйҐЬиЙ≤еЃЪдєЙжШѓйТИеѓєйҐЬиЙ≤зЪДжДЯзЯ•зЙєжАІеЃЪдєЙзЪДпЉМдЄФзФ±дЇОеРМиЙ≤еЉВи∞±пЉИе§ЪзІНдЄНеРМж≥ҐйХњзїДеИЖжЮДжИРзЪДеЕЙжШЊзО∞еЗЇзЫЄеРМзЪДйҐЬиЙ≤пЉЙзЪДзО∞и±°пЉМйҐЬиЙ≤дЄНжШѓж≥ҐйХњзЪДеФѓдЄАжШ†е∞ДпЉМеЫ†ж≠§дЄАзІНйҐЬиЙ≤дЄНиГљи°®з§ЇжЯРеНХдЄАж≥ҐйХњзЪДеЕЙгАВпЉИеНХдЄАж≥ҐйХњ жШѓ дЄАзІНйҐЬиЙ≤ зЪД еЕЕеИЖдЄНењЕи¶БжЭ°дїґпЉЙ
еЕ≥дЇОиЙ≤ељ©з©ЇйЧіпЉМжЫіе§ЪеЖЕеЃєиѓЈеПВиАГпЉЪ
1.Colorimetry: Understanding the CIE SystemпЉМдљЬиАЕJanos Schandaдї•ељУдЇЛдЇЇзЪДиІТеЇ¶иЃ≤иІ£CIEз≥їзїЯзЪДеїЇзЂЛеОЖз®ЛдЄОжЦєж≥ХгАВйЩДдЄКZ-libraryйУЊжО•пЉЪ
2.зЯ•дєО @зЂ†дљ≥жЭ∞ еЕ≥дЇОзЪДиЙ≤ељ©з©ЇйЧіжЦЗзЂ†
3.иЊРе∞ДеТМеЕЙеЇ¶
дїїдљХеЕЙжЇРпЉМжЧ†иЃЇжШѓдЇЇеЈ•еЕЙжЇРињШжШѓиЗ™зДґеЕЙжЇРпЉМжЬђиі®дЄКйГљжШѓе∞ЖеРДзІНеРДж†ЈзЪДиГљйЗПпЉИзФµиГљгАБеМЦе≠¶иГљз≠ЙпЉЙиљђеПШдЄЇеЕЙиГљйЗКжФЊпЉМиАМеЕЙзЪДиГљйЗПи∞±дї•еПКеКЯзОЗпЉМжШѓжЬЙеЕґиЃ°йЗПжЦєеЉПзЪДпЉЪиЊРе∞ДжµЛеЃЪпЉИRadiometryпЉЙеТМеЕЙеЇ¶жµЛеЃЪпЉИPhotometryпЉЙгАВ
Radiometry is the study of electromagnetic radiation. [7] иЊРе∞ДжµЛеЃЪжШѓеѓєзФµз£БиЊРе∞ДзЪДз†Фз©ґгАВж†єжНЃйЗПе≠РеКЫе≠¶зЪДж≥ҐеК®зРЖиЃЇпЉМиГљйЗПеПѓдї•еГПзФµз£Бж≥ҐдЄАж†ЈдЉ†жТ≠пЉМзФµз£Бж≥ҐзФ±зФµеЬЇеТМдЄАиµЈдЉ†жТ≠зЪДз£БеЬЇзїДжИРгАВзФµз£БиЊРе∞ДеПѓдї•дї•еЕЙйАЯеЬ®иЗ™зФ±з©ЇйЧідЄ≠дЉ†жТ≠пЉМзФµз£Бж≥ҐпЉИElectromagnetic wavesпЉЙеПѓдї•зФ®дЄНеРМзЪДзЙ©зРЖйЗПжЭ•и°®з§ЇпЉМдЊЛе¶Вж≥ҐйХњжИЦеКЯзОЗгАВ
Photometry is a subset of radiometry that deals with electromagnetic radiation that matters to the human being. еЕЙеЇ¶жµЛеЃЪжШѓиЊРе∞ДжµЛеЃЪзЪДдЄАдЄ™е≠РйЫЖпЉМзФ®дЇОе§ДзРЖеѓєдЇЇз±їйЗНи¶БзЪДзФµз£БиЊРе∞ДгАВеЬ®еЕЙеЇ¶жµЛеЃЪдЄ≠пЉМзФµз£БиЊРе∞ДеПѓдї•дљњзФ®дЇЇзЬЉзЪДжДЯзЯ•зЙєеЊБжЭ•и°®з§ЇгАВеЕЙеЇ¶жµЛеЃЪжШѓдЇЇзЬЉзЬЛеИ∞зЪДиЊРе∞ДжµЛйЗПпЉМеН≥еПѓиІБеЕЙеЕЙи∞±дЄ≠зЪДзФµз£БиЊРе∞ДгАВзЬЉзЭЫжШѓдЇЇз±їеФѓдЄАеПѓдї•зЬЛеИ∞зФµз£БиЊРе∞ДпЉИдї•еПКжХідЄ™дЄЦзХМпЉЙзЪДжОҐжµЛеЩ®пЉМзДґиАМзЬЉзЭЫдЄНиГљдї•зЫЄеРМжХПжДЯеЇ¶жДЯзЯ•жЙАжЬЙж≥ҐйХњпЉИжХідЄ™зФµз£Бж≥Ґи∞±пЉЙзЪДеЕЙпЉМзФЪиЗ≥дЇЇзЬЉж†єжЬђзЬЛдЄНеИ∞дЄАдЇЫж≥ҐйХњзЪДзФµз£Бж≥ҐгАВињЩ襀зІ∞дЄЇзЬЉзЭЫзЪДйЭЮзЇњжАІеЕЙи∞±еУНеЇФгАВдЇЇзЬЉеПѓдї•зЬЛеИ∞зЪДж≥ҐйХњиМГеЫізІ∞дЄЇеЕЙпЉИдєЯзІ∞дЄЇиІЖиІЙиѓДдЉ∞зЪДиЊРе∞ДиГљйЗПпЉЙпЉМж≠£еЄЄдЇЇзЬЉеПѓдї•жДЯзЯ•зЪДж≥ҐйХњиМГеЫідЄЇ380иЗ≥760 nmгАВеЫЊ11жШЊз§ЇдЇЖдЇЇз±їеѓєзФµз£БиЊРе∞ДзЪДиІЖиІЙеУНеЇФеѓєдЇОж≥ҐйХњзЪДеЗљжХ∞жЫ≤зЇњпЉМињЩ襀зІ∞дЄЇдЇЇзЬЉзЪДжШОиІЖиІЙеУНеЇФеЗљжХ∞пЉИthe photopic response functionпЉЙгАВ

еЫЊ11 Spectral Response of the Human Eye (also known as the luminous efficiency function).
зЫЄжѓФдєЛдЄЛпЉМеЫЇжАБжОҐжµЛеЩ®е∞Ждї•дЄНеРМзЪД嚥еЉПеУНеЇФиЊРе∞ДгАВе¶ВеЫЊ12жЙАз§ЇпЉМз°ЕеЕЙзԵ汆жОҐжµЛеЩ®пЉИsilicon photocell detector пЉЙеЬ®дЄНеРМж≥ҐйХњзЪДзФµз£БиЊРе∞ДдЄЛеЕЈжЬЙдЄОдЇЇзЬЉеЃМеЕ®дЄНеРМзЪДжХПжДЯеЇ¶

еЫЊ12 Spectral Response of a Typical Silicon Photocell
е¶ВеЫЊ11дЄОеЫЊ12жЙАз§ЇпЉМе¶ВжЮЬз°ЕеЕЙзԵ汆жОҐжµЛеЩ®еѓєдЇОзФµз£БиЊРе∞ДзЪДеПНеЇФдЄОдЇЇзЬЉзЪДеПНеЇФдЄНеМєйЕНпЉМеИЩдљњзФ®з°ЕеЕЙзԵ汆жОҐжµЛеЩ®ињЫи°МзЪДеЕЙжµЛйЗПеИЩдЄНз≠ЙеРМдЇОдЇЇзЬЉеѓєзЫЄеРМзФµз£Бж≥ҐзЪДеПНеЇФпЉМеЫ†ж≠§жѓПдЄ™еЕЙеЇ¶жµЛеЃЪйГљеЇФйАЪињЗж≠§жШОиІЖиІЙеУНеЇФеЗљжХ∞ињЫи°МеК†жЭГгАВзЙєеИЂеЬ∞пЉМдЇЇзЬЉеѓєиЊГзЯ≠еТМиЊГйХњзЪДж≥ҐйХњпЉИиУЭиЙ≤еТМзЇҐиЙ≤пЉЙзЪДеПНеЇФиЊГе∞ПпЉМеѓєдЄ≠йЧіж≥ҐйХњпЉИйїДиЙ≤еТМзїњиЙ≤пЉЙзЪДеУНеЇФиЊГйЂШгАВдЄЛи°®жАїзїУдЇЖеЕЙеЇ¶йЗПпЉИPhotometric quantityпЉЙеТМиЊРе∞ДйЗПпЉИRadiometric quantityпЉЙдєЛйЧізЪДеѓєеЇФеЕ≥з≥їпЉЪ

и°®1
еЕЙеЇ¶жµЛеЃЪдЄ≠зїЩеЃЪдЇЖиЃЄе§ЪдЄНеРМзЪДзЙ©зРЖйЗПгАВеЕЙеЇ¶жµЛеЃЪзЪДеЯЇжЬђеНХдљНжШѓеЭОеЊЈжЛЙпЉИcandela, cdпЉЙпЉМжИЦиАЕзІ∞дєЛдЄЇзГЫеЕЙгАВеЭОеЊЈжЛЙзЪДзђђдЄАдЄ™еЃЪдєЙжШѓзФ±еЕЙеЇ¶е≠¶еТМиЊРе∞ДжµЛйЗПе≠¶еІФеСШдЉЪпЉИthe Comite Consultatif de Photometrie et RadiometrieпЉМCCPRпЉЙдЇО1977еєізїЩеЗЇзЪДгАВеЬ®еЇ¶йЗПи°°е§ІдЉЪпЉИthe Conference Generale des Poids et MesuresпЉМCGPMпЉЙжЬЯйЧіпЉМеЃГ襀йЗНжЦ∞еЃЪдєЙпЉМеєґињЫи°МдЇЖдї•дЄЛе∞ПеєЕдњЃжФєпЉЪ
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 10^12 Hz and that has a radiant intensity in that direction of 1/683 Watts per Steradian (W/sr). еЭОеЊЈжЛЙжШѓеЕЙжЇРеЬ®зїЩеЃЪжЦєеРСдЄКзЪДеПСеЕЙеЉЇеЇ¶пЉМиѓ•еЕЙжЇРеПСе∞ДйҐСзОЗдЄЇ540 x 10^12 HzзЪДеНХиЙ≤иЊРе∞ДпЉМеєґдЄФиѓ•жЦєеРСзЪДиЊРе∞ДеЉЇеЇ¶дЄЇ1/683зУ¶жѓПзРГйЭҐеЇ¶пЉИW / srпЉЙгАВ 1cd=\frac{1}{683}W/Sr
The definition of candela applies for photopic, scotopic, and mesopic vision. The frequency 540 x 10^12 Hz corresponds to a wavelength of 555.016 nm in standard air. еЭОеЊЈжЛЙзЪДеЃЪдєЙйАВзФ®дЇОжШОиІЖгАБжЪЧиІЖеТМдЄ≠иІЖиІЖиІЙгАВйҐСзОЗ 540 x 10^12 Hz еѓєеЇФдЇОж†ЗеЗЖз©Їж∞ФдЄ≠ 555.016 nm зЪДж≥ҐйХњгАВ
жЧ©жЬЯзФ®дї•еИ§жЦ≠еЕЙжЇРи°®йЭҐзЪДжШОдЇЃз®ЛеЇ¶зЪДеЕЙдЊ¶жµЛеЩ®дїЕжЬЙдЇЇзЪДиВЙзЬЉдљЬдЄЇеЈ•еЕЈгАВељУжЧґзЪДдЇЇдїђдљњзФ®дЄАжФѓж†ЗеЗЖиЬ°зГЫеТМдЄАеП™еЊЕжµЛеЕЙжЇРдљЬжѓФиЊГпЉМеЕґдЄ≠дЄАеП™зЪДиЈЭз¶їеσ俕襀и∞ГжХіпЉМзЫіеИ∞дЄ§еП™еЕЙжЇР襀зЬЉзЭЫеИ§жЦ≠дЄЇеЕЈжЬЙзЫЄеРМзЪДжШОдЇЃз®ЛеЇ¶дЄЇж≠ҐпЉМеЖНзФ®еПНеє≥жЦєеЃЪеЊЛпЉИиІБ5.1иКВпЉЙиЃ°зЃЧеЗЇеЊЕжµЛеЕЙжЇРзЪДеЕЙеЉЇеЇ¶е§Іе∞ПгАВињЩдєЯжШѓдЄЇдїАдєИеЕЙзЪДеЯЇеЗЖиЃ°йЗПеНХдљНйЗЗзФ®еЕЙеЉЇеЇ¶иАМдЄНжШѓеЕґдїЦеЕЙеЇ¶жµЛеЃЪеНХдљНгАВйВ£жЧґжЙАдљњзФ®зЪДзЪДеЕЙеЉЇеЇ¶еНХдљНдЄЇзО∞еЈ≤дЄНеЖНдљњзФ®зЪДcandlepowerпЉМзЃАзІ∞cpпЉМжШѓжЧІеИґзЪДзГЫеЕЙеНХдљНпЉМдЄОзО∞дїКзЪДзГЫеЕЙcandleеЃЪдєЙдЄНеРМпЉМеЕґж†ЗеЗЖжШѓиЃЊиЃ°гАБзїУжЮДеТМжУНдљЬеЭЗеЕЈжЬЙзЙєеИЂиІДеЃЪзЪДиЬ°зГЫгАВ1860еєіиЛ±еЫље§ІйГљдЉЪ姩зДґж∞Фж≥Хж°ИдЄ≠еѓєcandlepowerеБЪеЗЇеЃЪдєЙпЉЪдЄАеП™ \frac{1}{6} з£ЕйЗНзЇѓй≤Єж≤єжЙАеИґзЪДиЬ°зГЫпЉМеЬ®жѓПе∞ПжЧґзЗГзГІ120ж†Љдї§пЉИgrainпЉЙзЪДйАЯеЇ¶дЄЛжЙАдЇІзФЯзЪДжШОдЇЃз®ЛеЇ¶пЉМдєЯ襀зІ∞дЄЇж†ЗеЗЖзГЫеЕЙгАВ[8] ињЩдєЯе∞±жШѓcandleињЩдЄАеНХдљНжЬАеИЭзЪДзФ±жЭ•пЉМж≠§й≤Єж≤єеПЦиЗ™жКєй¶Щй≤ЄзЪДе§ійГ®пЉМжЫЊдЄА寶襀зФ®жЭ•еИґйА†йЂШеУБиі®иЬ°зГЫгАВ

еЫЊ13
еРОжЭ•жђІзЊОеРДеЫљжФєдї•еРДзІНеРДж†ЈзЪДж≤єзБѓеПЦдї£иЬ°зГЫдљЬдЄЇеЕЙзЪДж†ЗеЗЖпЉМдЄАзЫіеИ∞1908еєіеЉАеІЛжЬЙзІСе≠¶еЃґиАГиЩСдї•зїЭеѓєйїСдљУжЭ•дї£жЫњзБѓдљЬдЄЇж†ЗеЗЖпЉМдљњзФ®зЩљйЗСеЗЭеЫЇзВєжЄ©еЇ¶зЪДйїСдљУиЊРе∞ДдљЬдЄЇеЕЙеЇ¶зЪДеЯЇжЬђеНХдљНгАВдєЛеРОзїПињЗдЄГеНБе§ЪеєізЪДжЉФеПШеРО嚥жИРдЇО1979еєіCGPMеЃЪдєЙзЪДcandleж†ЗеЗЖеНХдљНгАВ[9]

еЫЊ14
жЙАжЬЙзФ®дЇОеЕЙеЇ¶жµЛеЃЪзЪДеЕґдїЦеНХдљНйГљжЭ•жЇРдЇОеЭОеЊЈжЛЙзЪДеЃЪдєЙпЉМеМЕжЛђеЕЙйАЪйЗПпЉИLuminous FluxпЉЙгАБзЕІеЇ¶пЉИIlluminanceпЉЙгАБеПСеЕЙеЉЇеЇ¶пЉИLuminous IntensityпЉЙдЄОдЇЃеЇ¶пЉИLuminanceпЉЙгАВ
4.еЕЙйАЪйЗПгАБзЕІеЇ¶гАБеЕЙеЉЇдЄОдЇЃеЇ¶
A.еЕЙйАЪйЗПпЉИLuminous FluxпЉЙ \Phi_{V}
иЊРе∞ДиГљйЗПзЪДжЧґйЧіжµБйАЯпЉМж†єжНЃж†ЗеЗЖеМЦзЪДдЇЇз±їиІЖиІЙеПНеЇФпЉМеН≥иІЖиІЙеУНеЇФеЗљжХ∞ V_{\lambda} ињЫи°МиѓДдЉ∞пЉЪ
\Phi_{V}=K\int_{380}^{760}{\Phi}V_{\lambda}d\lambda\\\tag{15} еЕґдЄ≠пЉЪ
\Phi_V дЄЇеЕЙйАЪйЗПпЉМеНХдљНдЄЇжµБжШОпЉИlumenпЉЙ, 1Lumen=1cd\cdot sr
\Phi дЄЇиЊРе∞ДйАЪйЗПпЉМеНХдљНдЄЇзУ¶зЙє/зЇ≥з±≥пЉИW/nmпЉЙ
\lambda дЄЇж≥ҐйХњпЉМеНХдљНдЄЇзЇ≥з±≥пЉИnmпЉЙ
V_{\lambda} дЄЇиІЖиІЙеУНеЇФеЗљжХ∞
K дЄЇжЬАе§ІзЪДеЕЙи∞±еПСеЕЙжХИзОЗпЉМеНХдљНдЄЇжµБжШО/зУ¶зЙєпЉИLumen/WпЉЙгАВ K=683Lumen/W ,зФ±еПСеЕЙеЉЇеЇ¶зЪДSIеЫљйЩЕж†ЗеЗЖеЃЪдєЙгАВ
B.зЕІеЇ¶гАБеЕЙзЕІеЉЇеЇ¶пЉИIlluminanceпЉЙ E_{V}
жМЗеНХдљНйЭҐзІѓдЄКжЙАжО•еПЧеПѓиІБеЕЙзЪДеЕЙйАЪйЗПпЉЪ
E_{V}=\frac{d\Phi_V}{dA}\\\tag{16}
еЕґдЄ≠пЉЪ
E_{V} дЄЇзЕІеЇ¶пЉМеНХдљНдЄЇеЛТеЕЛжЦѓпЉИLuxгАБlxпЉЙпЉМ 1Lux=1 lumen/m^2
\Phi_V дЄЇеЕЙйАЪйЗПпЉМеНХдљНдЄЇжµБжШОпЉИlumenпЉЙ
C.еПСеЕЙеЉЇеЇ¶пЉИLuminous IntensityпЉЙ I_{V}
и°®з§ЇеЕЙжЇРеЬ®зїЩеЃЪжЦєеРСдЄКеНХдљНзЂЛдљУиІТеЖЕзЪДеЕЙйАЪйЗПпЉЪ
I_{V}=\frac{d\Phi_V}{d\omega}\\\tag{17} жХ∞е≠¶дЄКдЄАдЄ™зЂЛдљУиІТеЇ¶пЉИsolid angleпЉЙењЕй°їжЬЙдЄАдЄ™зВєдљЬдЄЇй°ґзВєпЉМеЫ†ж≠§еПСеЕЙеЉЇеЇ¶зЪДеЃЪдєЙдЄ•ж†ЉжДПдєЙдЄКеП™йАВзФ®дЇОзВєеЕЙжЇРгАВзДґиАМе¶ВжЮЬеЕЙжЇРзЪДе∞ЇеѓЄдЄОеЃГ襀иІВжµЛзЪДиЈЭз¶їзЫЄжѓФеПѓдї•ењљзХ•дЄНиЃ°пЉМйВ£дєИиѓ•еЕЙжЇРеσ俕襀聧䪯жШѓдЄАдЄ™зВєеЕЙжЇРдїОиАМеПѓдї•жППињ∞еЕґеПСеЕЙеЉЇеЇ¶гАВињЩйЗМзЪДзВєеЕЙжЇРињСдЉЉеМЕеРЂдї•дЄЛдЄ§дЄ™жЭ°дїґпЉЪ
- еЕЙжЇРеИ∞иІВжµЛдљНзљЃзЪДз©ЇйЧіиІТеЇ¶еПШеМЦжО•ињСдЇОиЈЭз¶їзЪДеє≥жЦєпЉИеН≥1.5еЕЙеЉЇжµЛеЃЪеЃЪеЊЛзЪДеПНеє≥жЦєеЃЪеЊЛпЉЙ
- дїОиІВжµЛдљНзљЃзЬЛеИ∞зЪДеЕЙжЇРжКХељ±еМЇеЯЯзЪДеє≥еЭЗдЇЃеЇ¶ж≤°жЬЙеПШеМЦ
D.дЇЃеЇ¶пЉИLuminanceпЉЙ L_{V}
дЇЃеЇ¶пЉИluminanceпЉЙеПИзІ∞иЊЙеЇ¶пЉМжШѓи°®з§ЇдЇЇзЬЉеѓєеПСеЕЙдљУжИЦ襀зЕІе∞ДзЙ©дљУи°®йЭҐзЪДеПСеЕЙжИЦеПНе∞ДеЕЙеЉЇеЇ¶еЃЮйЩЕжДЯеПЧзЪДзЙ©зРЖйЗПпЉЫеПѓзРЖиІ£дЄЇпЉЪеНХдљНйЭҐзІѓеЖЕзЬЛдЄКеОїжЬЙе§ЪдЇЃгАВељУдїїдЄ§дЄ™зЙ©дљУи°®йЭҐеЬ®зЕІзЫЄж״襀жЛНжСДеЗЇзЪДжЬАзїИзїУжЮЬжШѓдЄАж†ЈдЇЃгАБжИЦ襀зЬЉзЭЫзЬЛиµЈжЭ•дЄ§дЄ™и°®йЭҐдЄАж†ЈдЇЃпЉМеЃГдїђе∞±жШѓдЇЃеЇ¶зЫЄеРМгАВL_{V}=\frac{d^2\Phi_{V}}{d\Omega\cdot dA\cdot cos\theta}\\\tag{18} еЕґдЄ≠пЉЪ d дЄЇеЊЃеИЖзђ¶еПЈпЉМ \Omega дЄЇеПСеЕЙдљУжИЦ襀зЕІе∞ДзЙ©дљУи°®йЭҐдЄЇзРГењГзЪДзЂЛдљУиІТпЉМ dA дЄЇеПСеЕЙдљУжИЦ襀зЕІе∞ДзЙ©дљУи°®йЭҐйЭҐзІѓеЕГпЉМ \theta дЄЇ dA ж≥ХзЇњдЄО d\Omega жЦєеРСзЪДе§єиІТиІТеЇ¶пЉМзЂЛдљУеЗ†дљХеЕ≥з≥їе¶ВеЫЊ13жЙАз§ЇгАВ
пЉИзїіеЯЇзЩЊзІСгАБзЩЊеЇ¶зЩЊзІСзЪДеЕђеЉП L_{V}=\frac{d\Phi_{V}}{d\Omega\cdot d\cdot cos\theta} жЬЙзСХзЦµпЉМињЩйЗМдљњзФ®LighttoolsжУНдљЬжЙЛеЖМжПРдЊЫзЪДеЕђеЉПпЉМжѓФиЊГзђ¶еРИеѓєдЄ§дЄ™иЗ™еПШйЗПеЊЃеИЖзЪДжХ∞е≠¶и°®иЊЊгАВдЄ•ж†ЉжДПдєЙдЄКпЉМжИСиЃ§дЄЇеЇФиѓ•дљњзФ®еБПеЊЃеИЖзђ¶еПЈ \partialиАМдЄНжШѓеЊЃеИЖзђ¶еПЈ d пЉМдЄНињЗеѓєдЇОдЄАдЄ™зЙ©зРЖеЕ≥з≥їи°®иЊЊеЉПжЭ•иѓіжЧ†дЉ§е§ІйЫЕгАВпЉЙ

еЫЊ15
дЇЃеЇ¶еПѓиГљжШѓжЬАжť襀зРЖиІ£зЪДеЕЙеЇ¶йЗПгАВдЇЃеЇ¶пЉИLuminanceпЉЙзїПеЄЄеЬ®еЃЮйЩЕеЇФзФ®дЄ≠дЄОеЕЙеЉЇпЉИLuminous IntensityпЉЙгАБжШОдЇЃеЇ¶пЉИBrightnessпЉЙжЈЈжЈЖпЉМе∞§еЕґжШѓLuminanceдЄОBrightnessеЬ®е≠ЧеЕЄдЄ≠еЭЗжЬЙдЇЃеЇ¶зЪДйЗКдєЙгАВLuminanceжШѓдЄАдЄ™еЃҐиІВзЪДеЇ¶йЗПпЉМиАМBrightnessеИЩжШѓдЄАдЄ™дЄїиІВзЪДеЇ¶йЗПпЉМдЄФеПЦеЖ≥дЇОдЄїиІВдЄОзОѓеҐГељ±еУНгАВдї•дЄКзЪДдЇЃеЇ¶еЕђеЉПеПѓдї•зЃАеМЦдЄЇпЉЪL_{V}=\frac{I_V}{dA cos\theta}\\\tag{19} еЉЇеЇ¶ I_{V} жШѓдЇЃеЇ¶ L_{V} еТМеЕЙжЇРзЪДжКХељ±йЭҐзІѓ dAcos\theta зЪДдєШзІѓгАВињЩйЗМдњЭзХЩ dA зЪДи°®иЊЊжЦєеЉПпЉМеЫ†дЄЇињЩжШѓзФ±еПСеЕЙеЉЇеЇ¶ I_{V}еЉХзФ≥еЗЇжЭ•зЪДдЇЃеЇ¶пЉМеЫ†ж≠§дєЯйЬАи¶БйБµеЊ™еП™йАВзФ®дЇОзВєеЕЙжЇР/襀зЕІе∞ДзЙ©дљУи°®йЭҐзЪДињСдЉЉжЭ°дїґгАВе¶ВжЮЬз≥їзїЯдЄ≠ж≤°жЬЙеЕЙжНЯ姱пЉМйВ£дєИеЕЙжЇРзЪДдЇЃеЇ¶еЬ®иІВжµЛзВєдњЭжМБдЄНеПШпЉМињЩ襀зІ∞дЄЇдЇЃеЇ¶еЃИжБТпЉИ luminance conservationпЉЙгАВ
E.дЇЃеЇ¶еѓєжѓФеЇ¶пЉИLuminance ContrastпЉЙ C
дЇЃеЇ¶еѓєжѓФ寶襀еЃЪдєЙдЄЇпЉЪ
C=\frac{L_{Max}-L_{Min}}{L_{Max}+L_{Min}}\\\tag{20}
еЕґдЄ≠пЉЪ
L_{Max} дЄЇжЬАе§ІдЇЃеЇ¶
L_{Min} дЄЇжЬАе∞ПдЇЃеЇ¶
дї•дЄКеЕ≥дЇОеЕЙеЇ¶жµЛеЃЪзЪДеНХдљНеЬ®зЕІжШОињЗз®ЛдЄ≠и°°йЗПзЪДзЙ©зРЖйЗПеЭЗеЕЈжЬЙдЄНеРМжДПдєЙпЉМзФ±дЄЛеЫЊи°®з§ЇпЉЪ

еЫЊ16
еЕЙйАЪйЗПпЉИLuminous FluxпЉЙи°®з§ЇеЕЙжЇРдЇЇзЬЉжЙАиГљжДЯиІЙеИ∞зЪДиЊРе∞ДеКЯзОЗпЉЫ
еПСеЕЙеЉЇеЇ¶пЉИLuminous IntensityпЉЙи°®з§ЇеЕЙжЇРзїЩеЃЪжЦєеРСдЄКеНХдљНзЂЛдљУиІТеЖЕеЕЙйАЪйЗПзЪДзЙ©зРЖйЗПпЉЫ
зЕІеЇ¶пЉИIlluminanceпЉЙ谮积襀зЕІжШОи°®йЭҐеНХдљНйЭҐзІѓдЄКжЙАжО•еПЧеПѓиІБеЕЙзЪДеЕЙйАЪйЗПпЉЫ
дЇЃеЇ¶пЉИLuminanceпЉЙи°®з§ЇиІВжµЛдљНзљЃдЄКдЇЇз±їиІЖиІЙжДЯеПЧеИ∞зЪДгАБжЭ•иЗ™еПСеЕЙдљУжИЦ襀зЕІе∞ДзЙ©дљУи°®йЭҐзЪДеПСеЕЙжИЦеПНе∞ДеЕЙеЉЇеЇ¶еЃЮйЩЕжДЯеПЧзЪДзЙ©зРЖйЗПгАВ
пЉИдї•дЄКдЄ§иКВеЖЕеЃєзїЭе§ІйГ®еИЖеЉХзФ®иЗ™lighttoolsзЪДжУНдљЬжЙЛеЖМпЉМеєґз®НеК†жХізРЖгАВпЉЙ
5.еЕЙеЉЇжµЛйЗПеЃЪеЊЛ
A.еПНеє≥жЦєеЃЪеЊЛпЉИThe Inverse Square LawпЉЙ
еє≥жЦєеПНжѓФеЃЪеЊЛеЃЪдєЙдЇЖжЭ•иЗ™зВєжЇРзЪДиЊРзЕІеЇ¶дЄОиЈЭз¶їдєЛйЧізЪДеЕ≥з≥їгАВеЃГжМЗеЗЇжѓПеНХдљНйЭҐзІѓзЪДеЉЇеЇ¶дЄОиЈЭз¶їзЪДеє≥жЦєжИРеПНжѓФеПШеМЦпЉЪ
E=\frac{I}{d^2}\\\tag{21} еЕґдЄ≠ I дЄЇеПСеЕЙеЉЇеЇ¶пЉИ W or lm пЉЙпЉМ

еЫЊ17
B.йїЮеЕЙжЇРињСдЉЉпЉИPoint Source ApproximationпЉЙ
еє≥жЦєеПНжѓФеЃЪеЊЛеП™иГљеЬ®еЕЙжЇРињСдЉЉдЇОзВєеЕЙжЇРзЪДжГЕеЖµдЄЛдљњзФ®гАВзФ®дЇОиЊРзЕІеЇ¶жµЛйЗПзЪДдЄАиИђзїПй™Мж≥ХеИЩжШѓвАЬдЇФеАНж≥ХеИЩвАЭпЉЪеИ∞еЕЙжЇРзЪДиЈЭз¶їеЇФе§ІдЇОеЕЙжЇРжЬАе§Іе∞ЇеѓЄзЪДдЇФеАНгАВеѓєдЇОдЄАдЄ™йАПжШОзЪДеМЕзїЬзБѓпЉМињЩеПѓиГљжШѓзБѓдЄЭзЪДйХњеЇ¶пЉМеѓєдЇОз£®з†ВзБѓж≥°жЭ•иѓіпЉМзЫіеЊДжШѓжЬАе§ІзЪДе∞ЇеѓЄгАВдЄЛйЭҐзЪДеЫЊ6.2жШЊз§ЇдЇЖиЊРзЕІеЇ¶дЄОиЈЭз¶їдЄОжЇРеНКеЊДдєЛжѓФдєЛйЧізЪДеЕ≥з≥їгАВиѓЈж≥®жДПпЉМеѓєдЇОжЇРеНКеЊДзЪД10еАНпЉИзЫіеЊДзЪД5еАНпЉЙзЪДиЈЭз¶їпЉМдљњзФ®еє≥жЦєеПНжѓФзЪДиѓѓеЈЃж≠£е•љжШѓI%пЉМеЫ†ж≠§жШѓвАЬдЇФеАНвАЭињСдЉЉгАВ

еЫЊ18
еП¶иѓЈж≥®жДПпЉМељУиЈЭз¶їдЄОжЇРеНКеЊДзЪДжѓФзОЗйЩНиЗ≥0.1дї•дЄЛжЧґпЉИ20 еАНеЕЙжЇРзЪДзЫіеЊДпЉЙпЉМиЈЭз¶їзЪДеПШеМЦеЗ†дєОдЄНдЉЪељ±еУНиЊРзЕІеЇ¶пЉИиѓѓеЈЃе∞ПдЇО1%пЉЙгАВињЩжШѓеЫ†дЄЇйЪПзЭАдЄОеЕЙжЇРзЪДиЈЭз¶їеЗПе∞ПпЉМжОҐжµЛеЩ®зЬЛеИ∞зЪДйЭҐзІѓдЉЪеПШе∞ПгАВжКµжґИеє≥жЦєеПНжѓФеЃЪеЊЛгАВдЄКеЫЊеБЗиЃЊдљЩеЉ¶еУНеЇФгАВиЊРе∞ДжОҐжµЛеЩ®йЩРеИґиІЖеЬЇпЉМдљњ d/r жѓФзОЗеІЛзїИеЊИдљОпЉМжПРдЊЫдЄОиЈЭз¶їжЧ†еЕ≥зЪДжµЛйЗПгАВ
C.дљЩеЉ¶еЃЪеЊЛпЉИLambert&#39;s Cosine LawпЉЙ
иРљеЬ®дїїдљХи°®йЭҐдЄКзЪДиЊРзЕІеЇ¶пЉИirradianceпЉЙжИЦзЕІеЇ¶пЉИilluminanceпЉЙйЪПеЕ•е∞ДиІТ \theta зЪДдљЩеЉ¶иАМеПШеМЦгАВдЄОеЕ•е∞ДйАЪйЗПж≠£дЇ§зЪДжДЯзЯ•жµЛйЗПеМЇеЯЯеЬ®еАЊжЦЬиІТеЇ¶е§ДеЗПе∞ПпЉМдљњеЕЙжЙ©жХ£еИ∞жѓФеЮВзЫідЇОжµЛйЗПеє≥йЭҐжЫіеЃљзЪДеМЇеЯЯгАВе¶ВеЫЊ19жЙАз§ЇпЉМеѓєдЇОдЄНеРМиІТеЇ¶зЪДеЕЙжЭЯпЉМжКХе∞ДзЫЄеРМзЪДзЕІжШОйЭҐзІѓпЉМеЕґзЕІеЇ¶йБµеЊ™дљЩеЉ¶еЃЪеЊЛпЉЪ
E_\theta=E_{0}\ast cos(\theta)\\\tag{21} еЕґдЄ≠ E_{0} дЄЇеЕЙжЇРеЕЙжЭЯзЪДзЕІеЇ¶пЉМ \theta дЄЇеЕЙжЇРеЕЙжЭЯжЦєеРСдЄО襀зЕІжШОи°®йЭҐж≥ХзЇњзЪДе§єиІТпЉМ E_{\theta} 䪯襀зЕІжШОи°®йЭҐжО•еПЧеИ∞зЪДзЕІеЇ¶гАВ

еЫЊ19
D.жЬЧдЉѓи°®йЭҐпЉИLambertian surfaceпЉЙ
жЬЧдЉѓжЫ≤йЭҐжШѓдЄАзІНзРЖжГ≥зЪДгАБдїОжЙАжЬЙиІЖиІТжЦєеРСеСИзО∞еЭЗеМАжШОдЇЃеЇ¶дЄФеПНе∞ДеЕ®йГ®еЕ•е∞ДеЕЙзЪДеє≥йЭҐгАВињЩдЄ™еє≥йЭҐзЪДеПНе∞ДзОЗзІ∞дєЛдЄЇжЬЧдЉѓеПНе∞ДзОЗпЉИLambertian reflectanceпЉЙпЉМжШѓдЄАзІНзРЖжГ≥зЪДеУСеЕЙжИЦжЉЂеПНе∞Ди°®йЭҐжЙАеСИзО∞еЗЇзЪДзЙєжАІгАВе¶ВеЉПпЉИ22пЉЙжЙАз§ЇпЉМдЄНдЊЭиµЦдЇОиІВжµЛжЦєеРС \vec{s} гАБиЊРе∞ДеЬЇжИЦеЕЙжЇРдЇЃеЇ¶жБТеЃЪдЄЇ L гАБеЕ•е∞ДжЦєеРС \vec{r} пЉЪ
L(\vec{r},\vec{s})=L=constant\\\tag{22}
дїОдїїдљХжЦєеРСзЬЛпЉМжЬЧдЉѓжЫ≤йЭҐзЪДдЇЃеЇ¶пЉИBrightnessпЉЙйГљжШѓеЭЗеМАзЪДпЉМеН≥и°®йЭҐдЇЃеЇ¶жШѓеРДеРСеРМжАІзЪДгАВжЬЧдЉѓжЫ≤йЭҐйАЪ媪襀зІ∞дЄЇзРЖжГ≥жЙ©жХ£еє≥йЭҐпЉИIdeal Diffusion SurfacesпЉЙгАВеРДзІНи°®йЭҐзЪДеПНе∞ДдљњзФ®дїЦдїђзЪДеПМеРСеПНе∞ДеИЖеЄГеЗљжХ∞BRDFпЉИBidirectional reflectance distribution functionпЉЙеАЉжЭ•и°®з§ЇпЉМеЫ†дЄЇжЙАжЬЙжЬЧдЉѓжЫ≤йЭҐйГљйБµеЊ™жЬЧдЉѓдљЩеЉ¶еЃЪеЊЛпЉМеЫ†ж≠§жЬЧдЉѓжЫ≤йЭҐзЪДBRDFеАЉжШѓдЄАдЄ™еЄЄжХ∞еАЉгАВдєЯеЫ†дЄЇжЬЧдЉѓжЫ≤йЭҐйБµеЊ™жЬЧдЉѓдљЩеЉ¶еЃЪеЊЛпЉМдїОдЄОж≥ХзЇњ \vec{n} еСИе§єиІТ \theta зЪДжЦєеРСзЪДиЊРе∞ДеЉЇеЇ¶ I(\theta) дЄЇпЉЪ
I(\theta)=L\cdot A\cdot cos\theta=I_{0}\cdot cos\theta\\\tag{23}

еЫЊ20
дЇЛеЃЮдЄКпЉМиЃЄе§ЪжЉЂеПНе∞Ди°®йЭҐйГљжШѓжЬЧдЉѓи°®йЭҐгАВе¶ВжЮЬдљ†дїОдЄАеЃЪиМГеЫізЪДжЦЬиІТеЖЕзЬЛдЄАжЬђдє¶пЉМеЃГеЇФиѓ•зЬЛиµЈжЭ•еТМеЮВзЫідЇОдљ†зЪДиІЖзЇњжЧґдЄАж†ЈжШОдЇЃпЉМдЇЇзЬЉдї•еЕґжЬЙйЩРзЪДзЂЛдљУиІЖиІТжШѓзРЖжГ≥зЪДдЇЃеЇ¶жИЦдЇЃеЇ¶пЉИLuminance or BrightnessпЉЙжО•жФґеЩ®гАВ姙йШ≥еТМйїСдљУиЊРе∞ДзЫЄеѓєжО•ињСдЇОжЬЧдЉѓжЫ≤йЭҐгАВеЕЙзЕІи°®йЭҐйАЪеЄЄеЬ®йХЬйЭҐеПНе∞ДиІТпЉИSpecular angleпЉЙиМГеЫіеЖЕи°®зО∞еЗЇеҐЮеЉЇзЪДиЊРе∞ДеПСе∞ДзОЗпЉМеЫ†ж≠§дЄНеЃМеЕ®зђ¶еРИжЬЧдЉѓжЫ≤йЭҐзЪДжЭ°дїґгАВ
еЫЊ20еЈ¶еЫЊеЬ®еНКзРГдЄКињЫи°МзІѓеИЖеН≥еПѓиЃ°зЃЧжЬЧдЉѓеПНе∞ДзЪДжАїиЊРе∞ДеКЯзОЗпЉИ A дЄЇиЊРе∞ДйЭҐзІѓпЉЙпЉЪ
\Phi_{Lam}=\int I(\theta)d\Omega=L\cdot \int_{0}^{\frac{\pi}{b}}2\pi sin\theta\cdot cos\theta d\theta dA=\pi\cdot A\cdot L\\\tag{24} еѓєдЇОеНКе≠ФеЊДиІТпЉИHalf-aperture angle пЉЙ \varphi жЮДжИРзЪДеЕЙйФ•пЉЪ
\Phi_{Lam}=\pi\cdot A\cdot L\cdot sin^2\varphi=\pi\cdot I_{0}\cdot sin^{2}\varphi\\\tag{25} ж≠§еЕђеЉПзЙєеИЂйАВзФ®дЇОз©Їж∞ФдїЛиі®дЄ≠жХ∞еАЉе≠ФеЊДпЉИNAпЉЙиІТз≠ЙдЇО sin\varphi зЪДеЕЙе≠¶з≥їзїЯгАВ
еЬ®иАГиЩСеИ∞зБ∞дљУиЊРе∞ДжИЦиАЕжЫіжЩЃйБНзЪДеЕЙжЇРиЊРе∞ДеПСе∞ДзЪДиІТеЇ¶еИЖеЄГжЧґпЉМйЬАи¶БзФ®еИ∞еєњдєЙзЪДжЬЧдЉѓеПНе∞Дж®°еЮЛпЉЪ
I(\theta)=I_{0}\cdot cos^{m}\theta\\\tag{26} ељУ m=1 жЧґе∞±жШѓзїПеЕЄзЪДжЬЧдЉѓеПНе∞ДеИЖеЄГпЉМ mпЉЮ1 жППињ∞жЫіеЃЪеРСзЪДиЊРе∞ДзКґеЖµпЉМйЫЖдЄ≠дЇОж≥ХзЇњжЦєеРСгАВеѓєдЇОж≠§жЧґжАїиЊРе∞ДеКЯзОЗзЪДзІѓеИЖеЉПпЉМеПѓеЊЧпЉЪ
\Phi_{Lam}=\int I(\theta)d\Omega=L\cdot \int_{0}^{\frac{\pi}{b}}2\pi sin\theta\cdot cos^m\theta d\theta dA=\frac{\pi\cdot A\cdot L}{m+1}\\\tag{27} ињЩдЄ™еИЖеЄГзЪД嚥зКґе¶ВеЫЊ21гАБеЫЊ22жЙАз§ЇпЉЪ
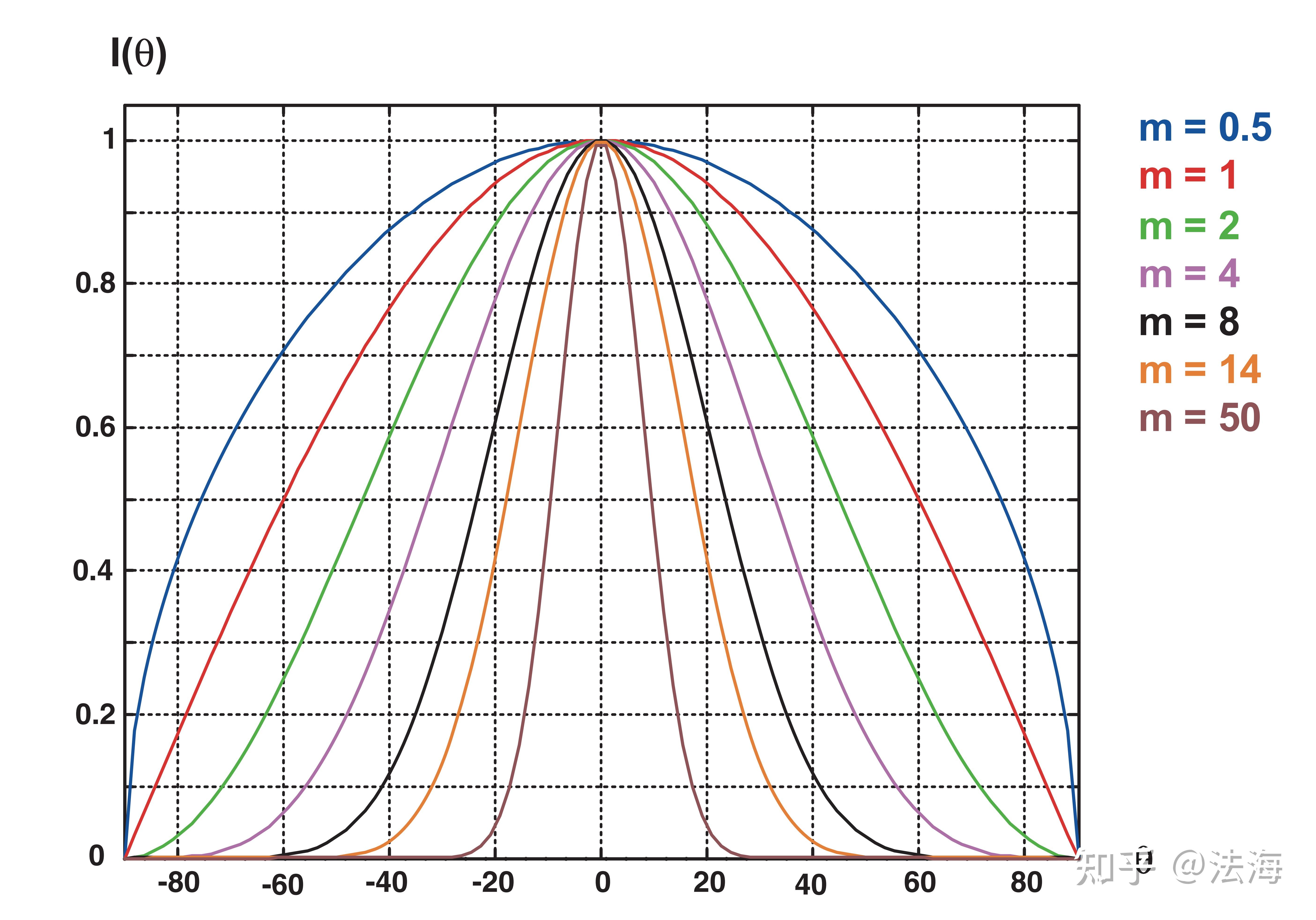
еЫЊ21 иЊРе∞ДеЉЇеЇ¶йЪПеАЊжЦЬиІТ ќЄ зЪДеЗљжХ∞иАМеПШеМЦ

еЫЊ22 иЊРе∞ДеЉЇеЇ¶зЪДжЮБеЭРж†ЗеЫЊ
дЄКињ∞嚥еЉПдЄЛзЪДиІТеИЖеЄГзЪДеєњдєЙжЬЧдЉѓеПНе∞ДпЉМдєЯеПѓдї•зФ®дЇОжЉЂеПНе∞ДйЭҐжИЦйАПе∞ДйЭҐзЪДжХ£е∞ДжАІиі®гАВеѓєдЇОйЗНи¶БзЪДеЃЮйЩЕжГЕеЖµпЉМжИСдїђеПѓдї•жЙЊеИ∞и°®2дЄ≠жЙАеИЧзЪДжМЗжХ∞mзЪДеАЉпЉЪ

и°®2
еЉХеЕ•еєњдєЙжЬЧдЉѓеПНе∞ДзЪДж¶ВењµпЉМеН≥еПѓеѓєжЙАжЬЙжЭРжЦЩзЪДеПНе∞ДзЙєжАІзФ®жЫіз≤ЊеЗЖзЪДеПВжХ∞ињЫи°МжППињ∞пЉМдїОиАМињЫи°МжЫіз≤Њз°ЃзЪДиЃ°зЃЧгАВ
дЇМгАБеЕЙжЇРзІНз±ї
еЕЙжЇРеПѓдї•еИЖдЄЇзЫЄеє≤еЕЙжЇРгАБйЭЮзЫЄеє≤еЕЙжЇРпЉМзЫЄеє≤еЕЙжЇРдЄїи¶БжШѓжњАеЕЙеЕЙжЇРпЉМйЭЮзЫЄеє≤еЕЙжЇРеМЕжЛђеПСеЕЙдЇМжЮБдљУпЉИLEDпЉЙгАБеЃљи∞±еЕЙжЇРпЉМеЕґдЄ≠еЃљи∞±еЕЙжЇРдЄїи¶БдЄЇзЩљзВљзБѓгАБеН§зі†зБѓз≠ЙжО•ињСдЇОйїСдљУиЊРе∞ДзЪДеЕЙжЇРгАВдЄ•ж†ЉжДПдєЙдЄКжЭ•иѓіпЉМйЭЮзЫЄеє≤еЕЙжЇРеєґйЭЮзїЭеѓєжДПдєЙдЄКзЪДеЃМеЕ®дЄНзЫЄеє≤пЉМеП™жШѓзФ±дЇОеЕґеЕЙи∞±иМГеЫіеЊИе§ІеѓЉиЗіеРМи∞ГйХњеЇ¶еЊИзЯ≠гАВ
1.зЩљзВљзБѓ Incandescent light bulb
зЩљзВљзБѓеПИеРНйТ®дЄЭзБѓпЉМйАЪињЗзїЩйТ®дЄЭеИґзЪДзБѓдЄЭйАЪзФµеК†зГ≠иЗ≥зЩљзГ≠пЉИзЩљзГ≠IncandescenceпЉМжМЗеѓєзЙ©дљУжЦљеК†иГљйЗПдљњеЕґжЄ©еЇ¶дЄКеНЗзЫіиЗ≥дЇІзФЯеПѓиІБеЕЙзЪДзО∞и±°пЉЙдЇІзФЯеЕЙжЇРпЉМйАЪеЄЄзФ®зОїзТГеИґжИРзБѓж≥°зїіжМБзБѓдЄЭзЪДзЬЯз©ЇзОѓеҐГжИЦиАЕдљОеОЛзЪДжГ∞жАІж∞ФдљУзОѓеҐГпЉМдї•дљЬйШ≤ж≠ҐзБѓдЄЭеЬ®йЂШжЄ©дЄЛж∞ІеМЦдєЛзФ®гАВзЩљзВљзБѓеЕЈжЬЙжО•ињСйїСдљУиЊРе∞ДзЪДеЕЙи∞±зЙєеЊБпЉМе¶ВеЫЊ21жЙАз§Ї[10]

еЫЊ21
е§ІйГ®еИЖзЩљзВљзБѓдЉЪжККжґИиАЧиГљйЗПдЄ≠зЪД90%иљђеМЦдЄЇзГ≠иГљпЉМеП™жЬЙ10%зЪДиГљйЗПдЉЪжИРдЄЇзФµз£БиЊРе∞Д/еЕЙгАВдєЯеЫ†ж≠§еЃЮй™МеЃ§дЄ≠зЪДзЩљзВљзБѓеЕЙжЇРйАЪеЄЄйГљйЕНжЬЙдљУзІѓиЊГе§ІзЪДжХ£зГ≠и£ЕзљЃпЉМеѓєдЇОжЄ©еЇ¶иЊГдЄЇжХПжДЯзЪДеЕЙжЬЇз≥їзїЯе§ДзРЖињЩдЄАзКґеЖµиЊГдЄЇйЇїзГ¶гАВ
зЩљзВљзБѓзЪДеЕЙзЇњдЄНдЉЪйЧ™зГБпЉМдЇ§жµБзФµзЪДзФµеОЛйЬЗиН°еП™дЉЪдљњйТ®дЄЭзЪДжЄ©еЇ¶жЬЙзХ•еЊЃзЪДйЬЗиН°пЉМеП™йЬАи¶Бж°•еЉПзФµиЈѓеѓєзФµжЇРињЫи°МзЃАеНХзЪДжХіжµБеН≥еПѓе∞ЖињЩдЇЫйЬЗиН°жґИеЗПиЗ≥еПѓењљзХ•дЄНиЃ°гАВзФ±дЇОзЩљзВљзБѓжО•ињСдЇОйїСдљУиЊРе∞ДпЉМеЫ†ж≠§еЕґиЙ≤ељ©и°®зО∞жЮБдљ≥пЉМеЕЈжЬЙеЊИе•љеЊЧжЉФиЙ≤жАІжМЗжХ∞пЉИCRIпЉЙи°®зО∞гАВ
2.еН§зі†зБѓ Halogen Lamp
еН§зі†зБѓжШѓе°ЂеЕЕжЬЙеН§жЧПеЕГзі†ж∞ФдљУпЉИйАЪеЄЄжШѓзҐШжИЦиАЕжЇіпЉЙзЪДзЩљзВљзБѓгАВељУзБѓдЄЭеПСзГ≠жЧґпЉМйТ®еОЯе≠Р襀еНЗеНОеРОеРСзБѓж≥°еЖЕе£БзІїеК®пЉМжО•ињСзБѓж≥°еЖЕе£БжЧґеЖЈеНіиЗ≥800вДГеєґдЄОеН§зі†еОЯе≠РзїУеРИеЬ®дЄАиµЈпЉМ嚥жИРеН§еМЦйТ®гАВеН§еМЦйТ®жµБеРСзОїзТГзЃ°дЄ≠е§ЃзїІзї≠зІїеК®пЉМеЫЮеИ∞襀ж∞ІеМЦзЪДзБѓдЄЭдЄКгАВзФ±дЇОеН§еМЦйТ®дЄНз®≥еЃЪпЉМдЇОзБѓдЄЭдЄКйБЗзГ≠еПИдЉЪйЗНжЦ∞еИЖиІ£дЄЇеН§зі†ж∞ФдљУеТМйТ®пЉМйТ®еОЯе≠РеЬ®зБѓдЄЭи°®йЭҐеЗЭеНОпЉМ劕谕襀еНЗеНОзЪДйГ®еИЖгАВйАЪињЗињЩзІНеЖНзФЯеЊ™зОѓпЉМзБѓдЄЭдљњзФ®еѓњеСље§Іе§ІеїґйХњпЉМеРМжЧґзФ±дЇОзБѓдЄЭеПѓдї•еЬ®жЫійЂШжЄ©еЇ¶дЄЛеЈ•дљЬпЉМеЫ†ж≠§еПѓдї•жПРдЊЫжЫійЂШзЪДиЙ≤жЄ©гАБжЫійЂШзЪДдЇЃеЇ¶еТМжЫійЂШзЪДеПСеЕЙжХИзОЗгАВ
зФ±дЇОеН§зі†зБѓеЈ•дљЬжЄ©еЇ¶еЊИйЂШпЉМжЩЃйАЪзОїзТГеЃєжШУиЮНеМЦжµБеК®пЉМеЫ†ж≠§дЉЪдљњзФ®зЯ≥иЛ±зОїзТГжЭ•дљЬдЄЇзБѓж≥°жЭРиі®гАВиАМжЩЃйАЪзОїзТГеЕЈжЬЙдЄАеЃЪзЪДйШїйЪФзіЂе§ЦзЇњзЪДиГљеКЫпЉМзЯ≥иЛ±зОїзТГйШїйЪФзіЂе§ЦзЇњзЪДиГљеКЫеЊИеЉ±пЉМеЫ†ж≠§еН§зі†зБѓеЕЙжЇРеЕЈжЬЙдЄАеЃЪзіЂе§ЦеЕЙж≥ҐжЃµзЪДдЄНеПѓиІБеЕЙгАВйЩ§дЇЖжУНдљЬйЬАи¶БињЫи°МзЫЄеЇФзЪДйШ≤жК§дї•е§ЦпЉМеЕЙе≠¶з≥їзїЯдЄ≠еН§зі†зБѓзЪДеЕЙеЉЇжОІеИґгАБжї§ж≥ҐжОІеИґдєЯйЭЮеЄЄйЗНи¶БпЉМдї•йШ≤ж≠ҐињЗйЂШзЪДеЕЙеЉЇе∞ЖеЕЙе≠¶еЕГдїґзГІеЭПпЉИжЙАжЬЙзЪДеЕЙе≠¶еЕГдїґпЉМйХАиЖЬгАБзЫЄжЬЇз≠ЙйГ®еИЖеЭЗжЬЙжЙњеПЧеЕЙзЕІеЉЇеЇ¶зЪДдЄКйЩРпЉЙгАВ

еЫЊ22 ThorLab OSL2еН§зі†еЕЙзЇ§зЕІжШОеЕЙжЇРдЄ≠OSL2BзБѓж≥°(иУЭзЇњ)дЄОOSL2IRеЕЙжЇРдЄ≠OSL2BIRзБѓж≥°(зЇҐзЇњ)зЪДеЕЙи∞±еЫЊ
йАЪеЄЄеЃЮй™МеЃ§дЄ≠дљњзФ®зЪДеН§зі†еЕЙжЇРйГљдЉЪдї•зБѓзЃ±зЪД嚥еЉПдљњзФ®пЉМе¶ВеЫЊжЙАз§ЇдЄЇThorLab OSL2еЕЙжЇРпЉМйАЪињЗеЕЙзЇ§иА¶еРИеРОзїПињЗдЄАжЭ°еЕЙзЇњжЭЯпЉИfiber bundleпЉЙ/еЕЙж≥ҐеѓЉпЉИlight guideпЉЙиЊУеЗЇпЉМйАЪињЗиљђжО•дїґеН≥еПѓжО•еЕ•еЕЙе≠¶з≥їзїЯдЄ≠гАВйАЪеЄЄжГЕеЖµдЄЛзБѓзЃ±йГљжЬЙиЗ™жИСдњЭжК§и£ЕзљЃпЉМйШ≤ж≠ҐзБѓзЃ±ињЗзГ≠[11]гАВ

еЫЊ23 ThorLab OSL2еЕЙжЇР
йАЙжЛ©еН§зі†зБѓзБѓзЃ±пЉМйЩ§дЇЖйЬАи¶Бж≥®жДПеЕґеЕЙи∞±гАБдЇЃеЇ¶дї•еПКеКЯзОЗдї•е§ЦпЉМињШйЬАи¶БиАГиЩСеЕґеЖЕзљЃжї§ж≥Ґи£ЕзљЃгАВдЊЛе¶ВпЉМOSL2зБѓзЃ±йҐДи£ЕOSL2BзБѓж≥°пЉМеЖЕзљЃзГ≠йХЬпЉМдї•йШїжМ°е§Іе§ЪжХ∞зЇҐе§ЦеЕЙпЉМеЕЄеЮЛж≥ҐйХњиМГеЫідЄЇ400 - 1600 nmпЉЫиАМеРМз±їеЮЛзЪДOSL2IRзБѓзЃ±йҐДи£ЕOSL2BIRзБѓж≥°пЉМеЄ¶жЬЙйУЭиЖЬеПНе∞ДйХЬпЉМдЄНеЄ¶зГ≠йХЬпЉМдї•еК†еЉЇињСзЇҐе§ЦиЊУеЗЇпЉМеЕЄеЮЛж≥ҐйХњиМГеЫідЄЇ400 - 1750 nmгАВ
3.жЧ•еЕЙзБѓ
жЧ•еЕЙзБѓжШѓдЄАзІНж∞ФдљУжФЊзФµзБѓпЉМдљњзФ®зФµеКЫеЬ®ж∞©жИЦж∞Цж∞ФдљУдЄ≠жњАеПСж∞ійУґиТЄж±љпЉМ嚥жИРзФµжµЖеєґеПСеЗЇзЯ≠ж≥ҐзіЂе§ЦзЇњпЉМзіЂе§Ц篜襀зІ∞дєЛдЄЇз£ЈеЕЙдљУзЪДиНІеЕЙжЭРжЦЩеРЄжФґеРОпЉМз£ЈеЕЙдљУдЉЪеПСеЗЇеПѓиІБеЕЙзФ®дї•зЕІжШОгАВж≠§з±їеПСеЗЇеПѓиІБеЕЙзЪДжЦєеЉПе±ЮдЇОиНІеЕЙпЉИfluorescenceпЉЙгАВ
иНІеЕЙжШѓдЄАзІНеЕЙиЗіеПСеЕЙпЉИPhotoluminescenceпЉЙпЉМе±ЮдЇОеЖЈеПСеЕЙзЪДдЄАзІНпЉМжМЗзЙ©иі®еРЄжФґеЕЙе≠Р/зФµз£Бж≥ҐеРОйЗНжЦ∞иЊРе∞ДеЗЇеЕЙе≠Р/зФµз£Бж≥ҐзЪДињЗз®ЛгАВељУжЯРзІНеЄЄжЄ©зЙ©иі®зїПињЗжЯРзІНж≥ҐйХњзЪДеЕ•е∞ДеЕЙпЉИйАЪеЄЄжШѓзіЂе§ЦзЇњжИЦXе∞ДзЇњињЩз±їеЕЈжЬЙиЊГйЂШиГљйЗПзЪДзФµз£Бж≥ҐпЉЙзЕІе∞ДпЉМеРЄжФґеЕЙиГљеРОињЫеЕ•жњАеПСжАБпЉМеєґдЄФзЂЛеН≥йААжњАеПСжАБеПСеЗЇеЗЇе∞ДеЕЙпЉИйАЪеЄЄжѓФеЕ•е∞ДеЕЙзЪДж≥ҐйХњиЊГйХњпЉЙгАВдЄАжЧ¶еБЬж≠ҐеЕ•е∞ДеЕЙпЉМеПСеЕЙзО∞и±°дєЯйЪПдєЛзЂЛеН≥жґИ姱гАВз£ЈеЕЙдЄОиНІеЕЙеПСеЕЙеОЯзРЖз±їдЉЉпЉМдЄАиИђдї•еПСеЕЙзЪДжМБзї≠жЧґйЧіжЭ•еИЖиЊ®дЇМиАЕпЉЪжМБзї≠еПСеЕЙжЧґйЧізЯ≠дЇО10^-8зІТзІ∞дєЛдЄЇиНІеЕЙпЉМжМБзї≠еПСеЕЙжЧґйЧійХњдЇО10^-8зІТзІ∞дєЛдЄЇз£ЈеЕЙгАВ

еЫЊ24 жЧ•еЕЙзБѓзЃ°
жЧ•еЕЙзБѓйЬАи¶БйЕНеРИзЫЄеЇФзЪДеЯЇеЇІгАБеРѓеК®зФµиЈѓгАБйХЗжµБеЩ®гАБеРѓиЊЙеЩ®дљњзФ®пЉМеЕґзФµиЈѓз§ЇжДПеЫЊе¶ВеЫЊ25жЙАз§ЇпЉМжЧ•еЕЙзБѓзЪДзФµиЈѓжЬЙеЊИе§ЪзІНињЩйЗМеП™еИЧдЄЊеЕґдЄ≠дЄАзІНпЉЪ

еЫЊ25 жЧ•еЕЙзБѓзФµиЈѓз§ЇжДПеЫЊ
ељУеЉАеЕ≥SйЧ≠еРИпЉМACзФµжЇРжО•еЕ•зФµиЈѓгАВйАЪзФµеЉАеІЛжЧґпЉМзФ±дЇОжЧ•еЕЙзБѓеЖЕж∞ійУґиТЄж±ље§ДдЇОдљОжЄ©зКґжАБеЊИйЪЊдЇІзФЯзФµжµБпЉМељУзФµеОЛиґ≥е§ЯжЧґеРѓиЊЙеЩ®зЪДжЮБзЙЗдЉЪй¶ЦеЕИдЇІзФЯжФЊзФµзЪДжГЕ嚥пЉМж≠§жЧґзФ±зФµеЃєдЄОйХЗжµБеЩ®зФµжДЯ嚥жИРзЪДLCжМѓиН°зФµиЈѓдЇІзФЯе§ІйЗПзФµжµБгАВзФµжµБйАЪињЗжЧ•еЕЙзБѓдЄ§зЂѓзЪДзБѓдЄЭдљњдЄ§зЂѓзЪДзБѓдЄЭеЭЗеЕЈжЬЙиґ≥е§ЯзЪДиГљйЗПжњАеПСзФµе≠Р嚥жИРзФµжµЖпЉМељУзФµжµЖ嚥жИРеРОжЧ•еЕЙзБѓзЃ°е∞±еПШжИРдЇЖзФµйШїеАЉиЊГдљОзЪДеѓЉдљУпЉМеЬ®еЖЕйî嚥жИРзФµе≠РжµБгАВзФ±дЇО嚥жИРзФµжµЖзЪДзБѓзЃ°зФµйШїињЬе∞ПдЇОеРѓиЊЙеЩ®пЉМеЫ†ж≠§еРѓиЊЙеЩ®зФµжµБдЄЛйЩНгАБжЮБзЙЗйЩНжЄ©жЦ≠еЉАпЉМжЧ•еЕЙзБѓзЃ°еЉАеІЛж≠£еЄЄеЈ•дљЬгАВж≠§жЧґе∞ЖеРѓиЊЙеЩ®жЛЖдЄЛдЄНдЉЪељ±еУНжЧ•еЕЙзБѓзЃ°еЈ•дљЬпЉМдЄАзЫіеИ∞зФµжЇРеЕ≥йЧ≠жЧ•еЕЙзБѓзЃ°жЙНдЉЪеБЬж≠ҐеЈ•дљЬгАВ
жЧ•еЕЙзБѓиҐЂеєњж≥ЫзФ®дЇОз©ЇйЧізЕІжШОпЉМиАМеЬ®еЃЮй™МеЃ§дЄ≠жЧ•еЕЙзБѓйАЪеЄЄдї•зОѓеҐГеЕЙзЪДиІТиЙ≤еЗЇзО∞гАВеѓєдЇОдЄАеЕЙе≠¶з≥їзїЯпЉМжИСдїђењЕй°їиАГиЩСзОѓеҐГеЕЙзЪДзїДеИЖзЪДељ±еУНгАВеѓєдЇОжЧ•еЕЙзБѓжИСдїђдЄїи¶БйЬАи¶БиАГиЩСдЄ§дЄ™ељ±еГПеЫ†зі†пЉЪжЧ•еЕЙзБѓеЕЙжЇРжШѓеР¶еЕЈжЬЙдЇ§жµБзФµйҐСзОЗзЪДйҐСйЧ™гАБжЧ•еЕЙзБѓеЕЙжЇРзЪДйҐСи∞±зїДеИЖгАВе¶ВеЫЊ24жЙАз§ЇдЄЇжЧ•еЕЙзБѓзЪДеЕЙи∞±еИЖжЮРеЫЊпЉМеЕґеЕЙи∞±иМГеЫіжґµзЫЦжХідЄ™еПѓиІБеЕЙж≥ҐжЃµеєґеЕЈжЬЙиЛ•еє≤е≥∞еАЉзїДеИЖгАВйАЪеЄЄжИСдїђдЉЪеЬ®жУНдљЬеЕЙе≠¶з≥їзїЯзЪДињЗз®ЛдЄ≠ињЫи°МйБЃеЕЙжИЦиАЕеЕ≥зБѓпЉМдї•иІДйБњзОѓеҐГеЕЙеѓєеЃЮй™МйА†жИРељ±еУНгАВ

еЫЊ26 жЧ•еЕЙзБѓеЕЙи∞±
4.ж∞ЩзБѓ Xenon Lamp
ж∞ЩзБѓжШѓеИ©зФ®еН§зі†ж∞ФдљУж∞Щж∞ФжФЊзФµеПСеЕЙзЪДеЕЙжЇРгАВж∞ЩзБѓзЪДеЕЙи∞±иГљйЗПеИЖеЄГдЄОжЧ•еЕЙжО•ињСпЉМиЙ≤жЄ©зЇ¶дЄЇ6000KгАВе¶ВеЫЊ27дЄЇThorLab SLS205ж∞ЩзБѓзЪДињЮзї≠еЕЙи∞±еИЖеЄГпЉМж∞ЩзЗИеЕЙи∞±еИЖеЄГеЗ†дєОдЄОзБѓзЪДиЊУеЕ•еКЯзОЗеПШеМЦжЧ†еЕ≥пЉМеЬ®еѓњеСљжЬЯеЖЕеЕЙи∞±иГљйЗПеИЖеЄГдєЯеЗ†дєОдЄНеПШпЉМеЕЈжЬЙз®≥еЃЪзЪДеПСеЕЙжАІиГљпЉМеЈ•дљЬзКґжАБеПЧе§ЦзХМжЭ°дїґеПШеМЦзЪДељ±еУНе∞ПгАВдЄФж∞ЩзБѓеЬ®зВєдЇЃдєЛеРОзЯ≠жЧґйЧіеЖЕеН≥еПѓиОЈеЊЧз®≥еЃЪзЪДеЕЙиЊУеЗЇпЉМдЄНйЬАи¶БйХњжЧґйЧізЪДйҐДзГ≠гАВж∞ЩзБѓзЪДеЕЙи∞±ж≥ҐжЃµжґµзЫЦдЇЖзіЂе§ЦзЇњеИ∞еПѓиІБеЕЙдї•еПКйГ®еИЖињСзЇҐе§ЦеЕЙеЕЙи∞±пЉИ240-1200nmпЉЙпЉМеЕЙи∞±ињЮзї≠дЄФеЭЗеЕЈжЬЙеЉЇеЇ¶гАВ

еЫЊ27 ThorLab SLS205ж∞ЩзБѓеЕЙи∞±
ж∞ЩзБѓдЊЭжНЃеКЯзОЗе§Іе∞ПдЄНеРМеИЖеИЂжЬЙй≥НзЙЗиЗ™зДґеЖЈеНігАБй£ОеЖЈеТМж∞іеЖЈзЪДеЖЈеНіж®°еЭЧпЉМйАЪеЄЄ3000~5000WдљњзФ®й£ОеЖЈпЉМжЫійЂШеКЯзОЗеИЩдљњзФ®ж∞іеЖЈгАВзФ±дЇОж∞ЩзБѓеЕЙзЇњеРЂжЬЙзіЂе§ЦзЇњдЄФеКЯзОЗиЊГйЂШпЉМеЫ†ж≠§еЬ®жУНдљЬињЗз®ЛдЄ≠йЬАи¶Бдљ©жИійАВељУзЪДйШ≤жК§зЬЉйХЬпЉМдЄФеЬ®жУНдљЬињЗз®ЛдЄ≠ж≥®жДПдЄНи¶БзЫіиІЖиЊУеЗЇзЂѓпЉМдєЯзХЩжДПдЄНи¶Бе∞ЖжЙЛжИЦзЪЃиВ§жФЊзљЃдЇОеЕЙиЈѓдЄКпЉМдї•йБњеЕН襀зБЉдЉ§гАВ

еЫЊ28 ThorLab SLS205ж∞ЩзБѓ
е¶ВеЫЊ28дЄ≠йЧіжЙАз§ЇпЉМеН≥дЄЇж∞ЩзБѓзЪДзБѓж≥°гАВжЧ†иЃЇжШѓж∞ЩзБѓињШжШѓеН§зі†зБѓпЉМзФ±дЇОзБѓж≥°йГљжШѓеЬ®зЫЄељУйЂШзЪДжЄ©еЇ¶дЄЛеЈ•дљЬзЪДпЉМдЄФеЭЗзФ±зЯ≥иЛ±зОїзТГеИґжИРпЉМеЫ†ж≠§йЬАи¶БдњЭжМБзБѓж≥°и°®йЭҐжЄЕжіБпЉМе¶ВжЮЬзОїзТГзЃ°е£Бж≤ЊжЯУж≤єж±°гАБзБ∞е∞ШпЉИдЊЛе¶ВзФ®жЙЛиІ¶жСЄзБѓж≥°пЉЙпЉМеИЩжЮБжШУеЬ®зБѓж≥°зВєдЇЃжЧґеЬ®и°®йݥ嚥жИРзГ≠жЦСпЉМдљњзЯ≥иЛ±зОїзТГиљђжНҐжИРжЩґдљУ嚥еЉПпЉМеПШеЊЧиДЖеЉ±жШУзҐОпЉМжШУеЉХиµЈеЖЕйГ®ж∞ФдљУж≥ДжЉПпЉМињШжЬЙеПѓиГљиµЈж≥°з†ізҐОгАВ
5.LED

еЫЊ29
еПСеЕЙдЇМжЮБдљУпЉИlight-emitting diodeпЉМLEDпЉЙжШѓдЄАзІНеНКеѓЉдљУеЕЙжЇРпЉМељУзФµжµБеНХеРСйАЪињЗжЧґеН≥еПѓеПСеЕЙпЉМеН≥дЄАзІНзФµиЗіеПСеЕЙзЪДеНКеѓЉдљУзФµе≠РеЕГдїґгАВLEDж†ЄењГзїУжЮДе∞±жШѓдЄАдЄ™P-NзїУжЮДжИРзЪДдЇМжЮБдљУпЉМдЄОжЩЃйАЪдЇМжЮБдљУдЄНеРМзЪДжШѓпЉМзФ±дЇОеЬ®еНКеѓЉдљУдЄ≠жОЇжЭВзЙєеЃЪзЪДеЕГзі†пЉМељУзФµе≠РдЄОзФµжіЮзїУеРИжЧґдЉЪжЬЙзФµз£БиЊРе∞ДеПСеЗЇпЉМеН≥зФµиЗіеПСеЕЙжХИеЇФгАВзФ±дЇОйЬАи¶БзФµе≠РдЄОзФµжіЮзїУеРИеПСеЗЇзФµз£БиЊРе∞ДпЉМеЫ†ж≠§еПСеЕЙдЇМжЮБдљУдїЕжЬЙй†ЖеБПзЪДP-NзїУжО•йЭҐдЄЛеЈ•дљЬпЉМдЄФеЊЃе∞ПзЪДй†ЖеБПзФµжµБеН≥еПѓдљњLEDеПСеЕЙпЉМеПСеЕЙеЉЇеЇ¶еЬ®дЄАеЃЪиМГеЫіеЖЕдЄОзФµжµБеЉЇеЇ¶еСИж≠£жѓФгАВеЕЙзЇњзЪДйҐЬиЙ≤дЄОеНКеѓЉдљУзЪДжЭРжЦЩгАБжОЇжЭВзЪДеЕГзі†жЬЙеЕ≥пЉМдЄїи¶БжЬЙвЕҐжЧПпЉИйУЭгАБйХУгАБйУЯпЉЙгАБвЕ§жЧПеЕГзі†пЉИж∞ЃгАБз£ЈгАБз†ЈпЉЙзїДжИРпЉМеПСе∞ДзЪДзФµз£Бж≥Ґж≥ҐйХњзФ±еОЯе≠РзЪДиГљйЪЩе§Іе∞ПеЖ≥еЃЪпЉМињЫиАМеЖ≥еЃЪдЇЖеПСеЕЙзЪДйҐЬиЙ≤гАВ
LEDеПѓдї•дЊЭдЇЃеЇ¶еИЖдЄЇдЄАиИђдЇЃеЇ¶зЪДдЉ†зїЯLEDпЉИдЄїи¶БзФ±GaPгАБGaAsPз≠ЙжЭРжЦЩжЮДжИРпЉЙпЉМйЂШдЇЃеЇ¶LEDпЉИAlGaAsпЉЙеПКиґЕйЂШдЇЃеЇ¶LEDпЉИInGaAlPгАБInGaNпЉЙгАВзФ±дЇОдЄНеРМеЕГзі†зЪДеОЯе≠РзЪДиГљйЪЩеЭЗжШѓеЫЇеЃЪзЪДпЉМеЫ†ж≠§дЇІзФЯзЪДзФµз£Бж≥ҐеЕЙи∞±еЕЈжЬЙзЫЄеЇФзЪДж≥Ґе≥∞зЙєеЊБгАВLEDеПѓдЇІзФЯзЪДзФµз£Бж≥ҐеМЕжЛђзіЂе§ЦзЇњгАБеПѓиІБеЕЙеТМзЇҐе§ЦзЇњж≥ҐжЃµпЉМжЮДйА†еТМеОЯзРЖзЫЄеРМпЉМеП™жШѓжЙАзФ®жЭРжЦЩжЬЙеЈЃеЉВгАВ
зЩљеЕЙLEDжШѓLEDеЕЙжЇРдЄ≠йЭЮеЄЄйЗНи¶БзЪДеПСжШОгАВвАЬзЩљеЕЙвАЭйАЪеЄЄжМЗе§ЪзІНйҐЬиЙ≤зЪДжЈЈеРИеЕЙпЉМдї•дЇЇзЬЉжДЯеЃШзЪДзЩљиЙ≤иЗ≥е∞СеМЕжЛђдЄ§зІНдї•дЄКзЪДж≥ҐйХњзїДеИЖпЉМдЊЛе¶ВиУЭиЙ≤еЕЙеК†йїДиЙ≤еЕЙпЉМиУЭиЙ≤еЕЙгАБзїњиЙ≤еЕЙгАБзЇҐиЙ≤еЕЙпЉМеЭЗеПѓиОЈеЊЧзЩљиЙ≤еЕЙгАВзЩљеЕЙLEDеЕЙжЇРзЪДдЇІзФЯдЄїи¶БжЬЙдї•дЄЛдЄЙзІНжЦєеЉПпЉЪ
- дї•зЇҐиУЭзїњдЄЙдЄ™еНХиЙ≤еЕЙдЇМжЮБдљУжЩґз≤ТзїДжИРзЩљеЕЙеПСеЕЙж®°зїДпЉМеЕЈжЬЙйЂШеПСеЕЙжХИзОЗгАБйЂШдїњиЙ≤жАІзЪДдЉШзВєпЉМдљЖеРМжЧґдєЯеЫ†дЄЇдЄНеРМйҐЬиЙ≤з£КжЩґжЭРжЦЩдЄНеРМпЉМдљњеЊЧзФЯдЇІињЗз®ЛдЄ≠жУНдљЬзФµеОЛдєЯдЄНеРМпЉМжОІеИґзЇњиЈѓиЃЊиЃ°е§НжЭВдЄФжЈЈеЕЙдЄНжШУпЉМеЫ†ж≠§жИРжЬђеБПйЂШгАВ

еЫЊ30
- жЧ•дЇЪеМЦе≠¶жПРеЗЇзЪДдї•иУЭеЕЙдЇМжЮБдљУжњАеПСйїДиЙ≤YAGиНІеЕЙз≤ЙдЇІзФЯзЩљеЕЙпЉМдЄЇзЫЃеЙНеЄВеЬЇзЪДдЄїжµБж®°еЉПгАВе¶ВеЫЊ31жЙАз§ЇпЉМеЬ®иУЭеЕЙLEDе§ЦеЫіе°ЂеЕЕжЈЈжЬЙйїДеЕЙYAGиНІеЕЙз≤ЙзЪДеЕЙе≠¶иГґпЉМж≠§иУЭеЕЙLEDдЇІзФЯж≥ҐйХњдЄЇ400-530nmзЪДиУЭеЕЙпЉМеИ©зФ®йГ®еИЖиУЭеЕЙжњАеПСYAGиНІеЕЙз≤ЙдЇІзФЯйїДиЙ≤еЕЙгАВињЩж†Јж≤°жЬЙеПВдЄОжњАеПСйїДеЕЙзЪДиУЭеЕЙдЄОйїДеЕЙдЄАеРМе∞ДеЗЇпЉМеН≥иОЈеЊЧжЈЈеРИжЬЙдЄ§дЄ™ж≥ҐйХњеЕЙзЪДзЩљеЕЙгАВж≠§зІНзЩљеЕЙLEDзЪДдЄїи¶БжЮДйА†пЉМеМЕеРЂеЇХйГ®зЪДиУЭеЕЙLEDжЩґзЙЗгАБжґВеЄГдЇОLEDжЩґзЙЗзЪДYAGйїДиЙ≤иНІеЕЙз≤ЙгАБдї•еПКйЪФзїЭе§ЦзХМзЪДзОѓж∞Іж†СиДВе∞Би£ЕгАВињЩзІНзЩљеЕЙLEDеЕЈжЬЙдї•дЄЛзЉЇзВєпЉЪ1.зФ±дЇОиУЭеЕЙеН†еПСеЕЙеЕЙи∞±зЪДе§ІйГ®еИЖпЉМеЫ†ж≠§дЉЪжЬЙиЙ≤жЄ©еБПйЂШдЄОдЄНеЭЗеМАзЪДзО∞и±°пЉМдЄЇж≠§ењЕй°їжПРйЂШиУЭеЕЙдЄОйїДеЕЙиНІеЕЙз≤ЙзЫЄдљЬзФ®зЪДжЬЇдЉЪпЉМдї•йЩНдљОиУЭеЕЙеЉЇеЇ¶жИЦжПРйЂШйїДеЕЙеЉЇеЇ¶пЉЫ2.еЫ†дЄЇиУЭеЕЙLEDеПСеЕЙж≥ҐйХњдЉЪйЪПзЭАжЄ©еЇ¶жПРеНЗиАМжФєеПШпЉМињЫиАМйА†жИРзЩљеЕЙеЕЙжЇРйҐЬиЙ≤жОІеИґдЄНжШУпЉЫ3.еЫ†еЕЙи∞±дЄ≠зЇҐиЙ≤ж≥ҐжЃµиЊГеЉ±пЉМйА†жИРдїњиЙ≤жАІпЉИcolor renditionпЉЙиЊГеЈЃзЪДзО∞и±°

еЫЊ31
- дї•зіЂе§ЦеЕЙLEDжњАеПСйАПжШОеЕЙе≠¶иГґдЄ≠дЊЭзЕІдЄАеЃЪжѓФдЊЛеЭЗеМАжЈЈеРИзЪДиУЭиЙ≤гАБзїњиЙ≤гАБзЇҐиЙ≤иНІеЕЙз≤ЙпЉМжњАеПСеРОеПѓиОЈеЊЧеЕЈжЬЙдЄЙзІНж≥ҐйХњзїДеИЖзЪДзЩљеЕЙгАВдЄЙж≥ҐйХњзЩљеЕЙжЛ•жЬЙзЫЄиЊГдЇОеЕґдїЦзЩљеЕЙLEDжЫійЂШзЪДжЉФиЙ≤жАІпЉМдљЖжШѓжЬЙеПСеЕЙжХИзОЗдЄНиґ≥зЪДзЉЇзВєгАВ
зФ®зіЂе§ЦеЕЙжИЦиУЭеЕЙжњАеПСиНІеЕЙз≤ЙиОЈеЊЧзЪДзЩљеЕЙеЕЙжЇРпЉМеЕґеЕ±еРМзЉЇзВєдЄЇеПСеЕЙдЇЃеЇ¶дЄНиґ≥дЄОеЭЗеМАеЇ¶жОІеИґдЄНжШУгАВзЫЃеЙНеЈ•дЄЪдЄ≠дї•еҐЮеК†йАПеЕЙеЇ¶дЄОдїОжЩґз≤ТеѓЉеЗЇжИЦж±≤еПЦжЫіе§ЪзЪДеПѓзФ®еПСеЕЙйЗПжЭ•иІ£еЖ≥LEDдЇЃеЇ¶дЄНиґ≥зЪДйЧЃйҐШгАВдЊЛе¶ВпЉМдљњзФ®йАПжШОеѓЉзФµжЭРжЦЩдї•еҐЮеК†жЩґз≤ТзЪДеЗЇеЕЙйЗПгАБжФєеПШжЩґз≤Тз£КжЩґжИЦзФµжЮБзїУжЮДиЃЊиЃ°дї•дЊњиОЈеЊЧжЫіе§ЪеПѓзФ®еПСеЕЙйЗПгАВ
еП¶е§ЦдљњзФ®зіЂе§ЦеЕЙLEDдљЬжњАеПСиНІеЕЙз≤ЙзЪДзЩљеЕЙеЕЙжЇРпЉМеЫ†зіЂе§ЦеЕЙеѓєдЇЇзЬЉжЬЙеЃ≥пЉМй°їе∞ЖзіЂе§ЦеЕЙйШїзїЭдЇОзЩљеЕЙLEDзїУжЮДеЖЕгАВжЧ•еЕЙзБѓйАЪињЗзОїзТГеИґзБѓзЃ°е∞ЖеЖЕйГ®зФµжµЖеПСе∞ДзЪДзіЂе§ЦзЇњйЪФзїЭпЉМиАМзіЂе§ЦеЕЙLEDдЄАжЦєйЭҐењЕй°їжПРеНЗиНІеЕЙз≤ЙзЪДзЩљеЕЙиљђжНҐжХИзОЗдЄОйШїзїЭзіЂе§ЦеЕЙе§ЦжЉПпЉМеП¶дЄАжЦєйЭҐжШѓеЄМжЬЫжФєињЫиНІеЕЙеПСеЕЙйЗПзЪДеРМжЧґдЇ¶еПѓжФєеЦДеПСеЕЙеЭЗеМАеЇ¶гАВ
дЄЇжФєеЦДдЄКињ∞дєЛзЉЇзВєпЉМеЬ®зЊОеЫљдЄУеИ©зђђ5962971еПЈдЄ≠дљњзФ®зіЂе§ЦеЕЙжї§ж≥ҐеЩ®пЉИUV filterпЉЙдљЬдЄЇLEDиНІеЕЙз≤Йе±ВеЕЙзЪДеЗЇе∞ДйЭҐзЪДе∞Би£ЕгАВж≠§жЦєеЉПеН≥еҐЮеК†иНІеЕЙз≤Йе±ВзЪДеПСеЕЙеЭЗеМАеЇ¶е§ЦеПИеПѓеРЄжФґйШїзїЭLEDзіЂе§ЦзЇњеѓєдЇЇзЬЉзЪДдЉ§еЃ≥гАВ
еП¶е§ЦеЬ®й£Юеȩ浶жЙАзФ≥иѓЈзЪДзЊОеЫљдЄУеИ©зђђ5813753еПЈеИЩжШѓеЬ®зіЂе§ЦеЕЙ/иУЭеЕЙLEDзЪДеПСеЕЙйЭҐдЄКйХАдЄКдЄАе±ВзЯ≠ж≥Ґз©њйАПжї§ж≥ҐеЩ®пЉИshort wave pass filterпЉЙпЉМдї•еҐЮеЉЇеПСеЕЙжЩґзЙЗзЪДзіЂе§ЦеЕЙеЗЇе∞ДйЗПдЄОLEDеПСеЕЙйЭҐзЪДеПѓиІБеЕЙ/иНІеЕЙеПНе∞ДйЗПпЉЫеП¶дЄАжЦєйЭҐеЬ®зіЂеЕЙ/иУЭеЕЙLEDзЪДеЙНзЂѓе∞ДеЗЇйЭҐзФ®еПѓиІБеЕЙз©њйАПжї§ж≥ҐеЩ®пЉИlong wave pass filterпЉЙдљЬе∞Би£ЕпЉМдї•еҐЮеК†еПѓиІБеЕЙз©њйАПзОЗгАВ
еЬ®зЊОеЫљдЄУеИ©зђђ6833565еПЈеИЩжШѓдљњзФ®еЕ®жЦєдљНеПНе∞ДзЙЗ嚥жИРдЄАдЄ™з±їдЉЉеЕ±жМѓиЕФзЪДжњАеПСиЕФзїУжЮДпЉМе∞ЖзіЂе§ЦеЕЙйЩРеИґеЬ®иНІеЕЙз≤ЙдЄ≠пЉМдї•жПРйЂШLEDзЪДеПСеЕЙжХИзОЗгАВ
LEDж†єжНЃйЬАж±ВгАБеПСеЕЙеУБиі®еЈЃеЉВпЉМжЬЙеЊИе§ЪзІНзІНз±їзЪДдЇІеУБгАВе¶ВThorLabдЇІеУБеЮЛељХдЄ≠еѓєLEDзЪДеИЖз±їпЉМеЫЊ32дЄЇжЬ™еЃЙи£ЕзЪДLEDзБѓж≥°дї•еПКйЕНеРИзЪДеЃЙи£ЕеЇІгАВ

еЫЊ32
еЈ≤еЃЙи£ЕеЃЙи£ЕеЇІзЪДLEDеПѓдљЬдЄЇеЕЙжЇРеЃЙи£ЕеЬ®еЕЙе≠¶з≥їзїЯдЄКпЉМе¶ВеЫЊ33жЙАз§ЇдЄЇеЈ≤еЃЙи£ЕеЃЙи£ЕеЇІзЪДLEDпЉМеПѓдї•зЫіжО•жО•еЕ•Thorlab CernaжШЊеЊЃз≥їзїЯ[12]пЉМдљЬиАЕз°Хе£ЂжЬЯйЧіжЙАеЬ®еЃЮй™МеЃ§иЗ™з†ФзЪДзЩљеЕЙжЙЂжППеє≤жґЙдї™пЉИеЫЊ34пЉЙдєЯжШѓдљњзФ®ж≠§зІНLEDзЩљеЕЙеЕЙжЇР[13]гАВ

еЫЊ33

еЫЊ34
еП¶е§ЦеЬ®йЂШз®≥еЃЪжАІгАБйЂШеУБиі®зЪДLEDеЕЙжЇРдЄКпЉМйАЪеЄЄдЉЪйЕНе•Чдї•зФ®жЦЩжЙОеЃЮгАБдљУзІѓиЊГе§ІзЪДжОІеИґзФµиЈѓдї•еПКеЕЙжЬЇз≥їзїЯпЉМдї•зБѓзЃ±зЪД嚥еЉПйАЪињЗеЕЙж≥ҐеѓЉиЊУеЗЇеЕЙжЇРгАВеЫЊ35дЄЇREVOX SLG-165V LEDзБѓзЃ±пЉМдЄЇжЬђдЇЇз°Хе£ЂиЃЇжЦЗдЄ≠еЃЮй™МжЙАзФ®еЕЙжЇР[14]гАВ

еЫЊ35 REVOX SLG-165V LED
6.ж∞ійУґзБѓ
ж∞ійУґзБѓеПИзІ∞ж±ЮзБѓпЉМеЖЕйГ®еРЂжЬЙж±ЮиТЄж∞ФпЉМдї•ж∞ФдљУжФЊзФµзЪДжЦєеЉПдЇІзФЯеЕЙжЇРгАВзБѓзЃ°дљњзФ®иАРзГ≠зОїзТГеИґжИРпЉМдЄ§зЂѓи£ЕжЬЙзФµжЮБпЉМеИґйА†дЄ≠жКљеОїз©Їж∞ФеЕЕеЕ•ж∞ійУґдї•еПКе∞СйЗПж∞©ж∞ФгАВйАЪзФµеРОж∞ійУґиТЄеПСдЄЇиТЄж±љпЉМж±ЮиТЄж∞ФеПЧзФµе≠РжњАеПСиАМеПСеЕЙгАВдЊЭзЕІзБѓзЃ°еЖЕж∞ійУґиТЄж±љзЪДеОЛеКЫе§Іе∞ПпЉМеИЖдЄЇдљОеОЛгАБйЂШеОЛеТМиґЕйЂШеОЛдЄЙзІНз±їеЮЛгАВдљОеОЛж∞ійУґзБѓеПСеЗЇеЉЇзіЂе§ЦеЕЙпЉМеН≥жИСдїђжЧ•еЄЄиІБеИ∞зЪДжЭАиПМзБѓзЪДзБѓзЃ°пЉЫж≠§з±їзБѓзЃ°еЖЕе£БжґВдї•иНІеЕЙжЭРжЦЩеРОеН≥жШѓжЧ•еЕЙзБѓгАВ
йЂШеОЛж∞ійУґзБѓеПСеЕЙжХИзОЗйЂШгАБдљњзФ®еѓњеСљйХњпЉМеЕЙи∞±зїДеИЖзіЂе§ЦеЕЙиЊГе§ЪгАБзЇҐеЕЙиЊГе∞СпЉМеПѓзФ®дљЬжЩТеЫЊжЬЇеЕЙжЇРпЉЫзБѓзЃ°еЖЕе£БжґВдї•иНІеЕЙзЙ©иі®еРОеПѓдЇІзФЯзЩљеЕЙпЉМеН≥йЂШеОЛж∞ійУґиНІеЕЙзБѓгАВиґЕйЂШеОЛж∞ійУґзБѓиТЄж±љеОЛеКЫеМЇйЧідЄЇ10133пљЮ20265KPa(100пљЮ200atm)пЉМдЄїи¶БеПСе∞Дж≥ҐйХњеЬ®546.1nmпЉИ130atmпЉЙгАВ
зФ±ж∞ійУґзБѓйЗСе±ЮеН§еМЦзБѓгАБйЂШеОЛйТ†зБѓгАБдљОеОЛйТ†зБѓйЂШеОЛж∞ійУґзБѓдї•еПКзЯ≠еЉІж∞ЩзБѓеЉХзФ≥еПСе±ХеЗЇйЂШеЉЇеЇ¶ж∞ФдљУжФЊзФµзБѓпЉИHigh-intensity dischargeпЉМHIDпЉЙпЉМж≠§з±їеЕЙжЇРеЭЗдї•еЖЕеЃєзЙ©йАЪзФµеРОдЇІзФЯзЪДзФµжµЖдљУдљЬдЄЇеПСеЕЙдљУпЉМдЇІзФЯйЂШдЇЃеЇ¶гАБйЂШеУБиі®гАБе§ІйЭҐзІѓзЪДзЕІжШОеЕЙжЇРгАВе¶ВеЫЊ36жЙАз§ЇпЉМжШѓдЄАдЄ™дљњзФ®еЬ®IMAXжКХељ±жЬЇдЄКзЪД15KWзЯ≠еЉІж∞ЩзБѓ[15]гАВ

еЫЊ36 дљњзФ®еЬ®IMAXжКХељ±жЬЇдЄКзЪД15KWзЯ≠еЉІж∞ЩзБѓ
зФ±дЇОHIDдљЬдЄЇзФµжµЖдљУзЪДйГ®еИЖзЙ©иі®жЧ†ж≥ХзЫіжО•йАЪињЗжЦљеК†зФµеОЛиОЈеЊЧжњАеПСзФµжµЖжАБзЪДиГљйЗПпЉМеЫ†ж≠§дЄОиНІеЕЙзБѓз±їдЉЉпЉМйАЪеЄЄзФ®зђђдЄЙдЄ™зФµжЮБеЬ®еЕґдЄ≠дЄАдЄ™дЄїзФµжЮБжЧБиЊєиЊЕеК©еРѓеК®пЉМдЊЛе¶Вж∞ійУґзБѓеТМдЄАдЇЫйЗСе±ЮеН§еМЦйТ®зБѓгАВиАМеЕґдїЦеЃєжШУйАЪињЗжЦљеК†зФµеОЛжњАеПСзФµжµЖжАБзЪДзБѓзІНеИЩйАЪеЄЄдљњзФ®йЂШеОЛиДЙеЖ≤зЪД嚥еЉПеРѓеК®гАВ
HIDйАЪеЄЄзФ®дЇОе§ІйЭҐзІѓзЕІжШОпЉМдї•еПКиѓЄе¶ВжЄ©еЃ§гАБж∞іжЧПй¶Жз≠ЙйЬАи¶Бж®°жЛЯеЉЇжЧ•еЕЙзЕІжШОгАБдЄФйЬАи¶БзїіжМБиЊГйЂШеЃ§жЄ©зЪДз©ЇйЧіпЉМеЬ®е¶ВдїКе§ЬзФЯжіїеПСиЊЊзЪДзО∞дї£з§ЊдЉЪдЇ¶еЄЄзФ®дЇОеїЇз≠СеЖЕе§ЦзЕІжШОгАВйГ®еИЖHIDпЉМдЊЛе¶Вж∞ійУґзБѓдЉЪжФЊеЗЇе§ІйЗПзіЂе§ЦзЇњпЉМеЫ†ж≠§йЬАи¶БжЙ©жХ£жЭњпЉИDiffusersпЉЙжЭ•йШїжМ°зіЂе§ЦзЇњзЪДиЊРе∞ДгАВ
7.жњАеЕЙ/йХ≠е∞Д/йЫЈе∞Д Laser
жњАеЕЙпЉИLightAmplification byStimulatedEmission ofRadiationпЉМLaserпЉЙжШѓвАЬйАПињЗеПЧжњАиЊРе∞ДдЇІзФЯзЪДеЕЙжФЊе§ІвАЭпЉМжМЗйАПињЗеИЇжњАеОЯе≠РеѓЉиЗізФµе≠РиЈГињБйЗКжФЊиЊРе∞ДиГљйЗПиАМдЇІзФЯзЪДеЕЈжЬЙеРМи∞ГжАІзЪДеҐЮеЉЇеЕЙе≠РжЭЯгАВеЕґзЙєзВєеМЕжЛђеПСжХ£еЇ¶жЮБе∞ПгАБдЇЃеЇ¶пЉИеКЯзОЗпЉЙеЊИйЂШгАБеНХиЙ≤жАІе•љгАБзЫЄеє≤жАІе•љз≠ЙгАВдЇІзФЯжњАеЕЙйЬАи¶БвАЬжњАеПСжЭ•жЇРвАЭгАБвАЬеҐЮзЫКдїЛиі®вАЭгАБвАЬеЕ±жМѓзїУжЮДвАЭињЩдЄЙдЄ™и¶Бзі†гАВ
жњАеЕЙдЇІзФЯзЪДеОЯзРЖиѓ¶иІБFPеЕ±жМѓиЕФпЉМжњАеЕЙзЪДйЂШеНХиЙ≤жАІгАБдљОеПСжХ£жАІгАБйЂШеЉЇдЇЃеЇ¶дЄОйЂШеРМи∞ГжАІеЭЗжЭ•иЗ™FPеЕ±жМѓиЕФпЉЪ
жњАеЕЙдЊЭжНЃжњАеПСдїЛиі®жИРеИЖеПѓдЄїи¶БеИЖдЄЇдї•дЄЛдЄГе§Із±їпЉЪ
вС†ж∞ФдљУжњАеЕЙпЉЪ
е¶Ви°®3жЙАз§ЇпЉМж∞ФдљУйХ≠е∞ДеИЖз±їпЉЪ
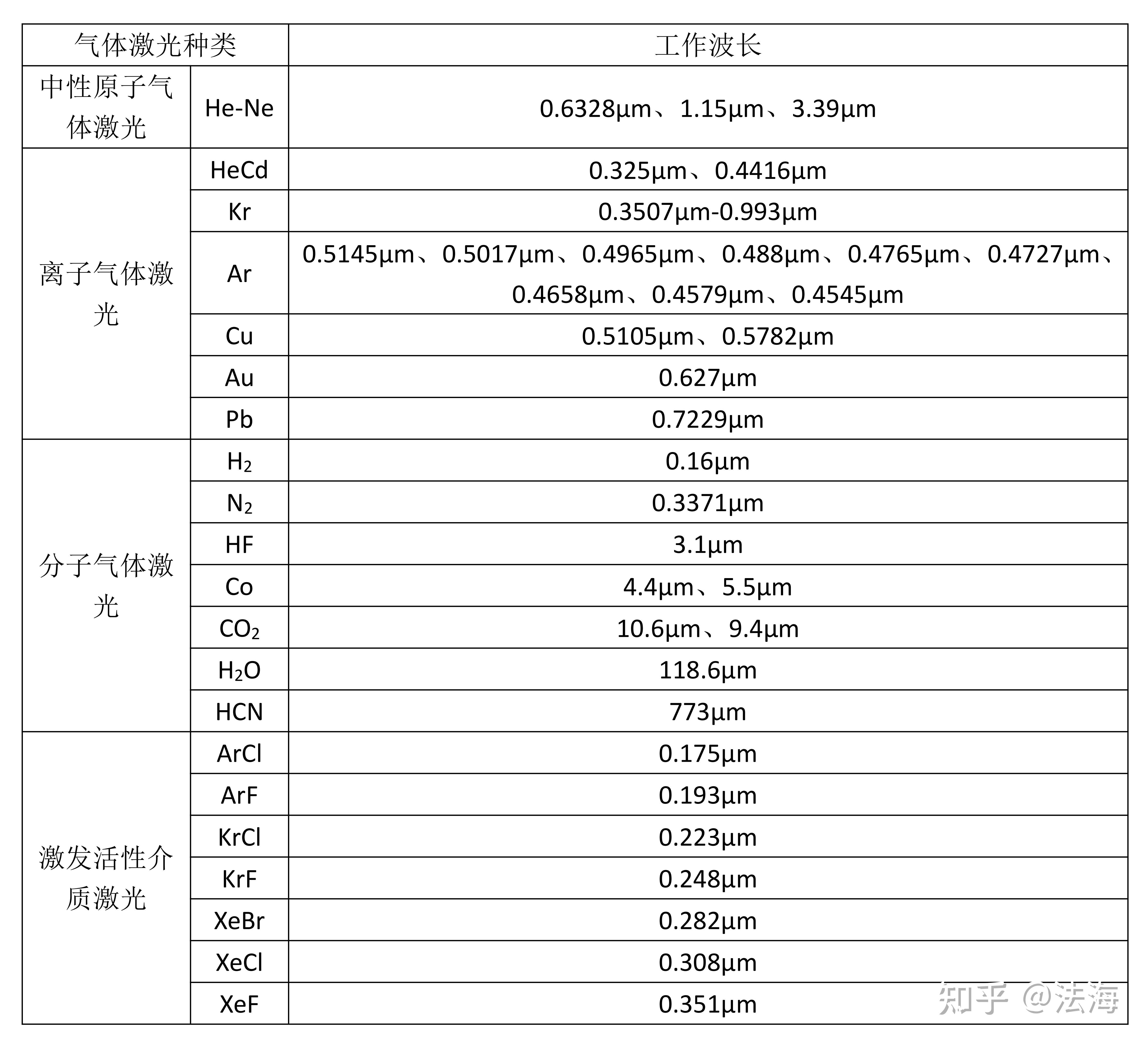
и°®3 ж∞ФдљУжњАеЕЙзІНз±ї
еЕґдЄ≠He-NeжњАеЕЙпЉИ633nmгАБ1.55ќЉmпЉЙиЊУеЗЇз®≥еЃЪпЉМж®™ж®°пЉИtransverse modeпЉЙ TEM_{00} еЕЙжЭЯпЉИеЫЊ37пЉЙпЉМ633nmдљНдЇОеПѓиІБеЕЙж≥ҐжЃµпЉМеРМи∞ГжАІйЂШпЉМеЫ†ж≠§еЄЄзФ®дЇОеЕЙзФµз≥їзїЯж†°ж≠£гАВ

еЫЊ37 TEMж®°еЉПеРДзІНиГљйЗПеИЖеЄГ
з¶їе≠Рж∞ФдљУ Ar^{+} дЄО Kr^{+} жњАеЕЙзЪДйҐСи∞±еИЖеЄГдЇОеПѓиІБеЕЙеМЇеЯЯпЉМеЕЈжЬЙдљОеПСжХ£иІТеТМиЙѓе•љзЪДеРМи∞ГжАІпЉМеПѓйАЪињЗж£±йХЬж≥ҐйХњйАЙжЛ©еЩ®и∞ГжХідЄЇеНХдЄАж≥ҐйХњиЊУеЗЇпЉМеЇФзФ®дЇОеЕ®еГПжЬѓеТМеЕЙи∞±дї™гАВ
еП¶е§ЦеЬ®еИЖе≠Рж∞ФдљУйХ≠е∞ДдЄ≠пЉМдЇМж∞ІеМЦзҐ≥жњАеЕЙпЉИ10.6ќЉmпЉЙзЪДжХИзОЗйЂШгАБињЮзї≠иЊУеЗЇеКЯзОЗе§ІпЉМеЄЄдљЬдЄЇжњАеЕЙеИЗеЙ≤зЪДеЕЙжЇРгАВж∞Ѓж∞ФжњАеЕЙпЉИ337.1nmпЉЙеЬ®йЂШиДЙеЖ≤йЗНе§НжѓФдєЛдЄЛеПѓдЇІзФЯзЯ≠иДЙеЖ≤пЉИе•ИзІТиЗ≥еЊЃзІТзЇІпЉЙйЂШе≥∞еАЉеКЯзОЗиЊУеЗЇпЉМеЄЄзФ®дЇОеПѓи∞Гж≥ҐйХњзЪДжЬЙжЬЇжЯУжЦЩжњАеЕЙеЩ®зЪДж≥µжµ¶еЕЙжЇРгАВ
вС°еЫЇдљУжњАеЕЙпЉЪ
еЫЇдљУжњАеЕЙйЗЗзФ®еЫЇжАБзЪДжіїжАІдїЛиі®пЉМжККеЕЈжЬЙдЇІзФЯеПЧжњАеПСе∞ДдљЬзФ®зЪДз¶їе≠РжОЇжЭВеЕ•жЩґдљУжИЦзОїзТГгАВеЫЇдљУжЭРжЦЩдЄ≠иГље§ЯдЇІзФЯеПЧжњАеПСе∞ДзЪДйЗСе±Юз¶їе≠РдЄїи¶БжЬЙдЄЙз±їпЉЪa.ињЗжЄ°йЗСе±Юз¶їе≠РпЉМдЊЛе¶В Cr^{3+} пЉЫb.е§Іе§ЪжХ∞зЪДйХІз≥їйЗСе±Юз¶їе≠РпЉМдЊЛе¶В Nd^{3+} гАБSm^{2+} гАБ Dy^{2+} з≠ЙпЉЫc.йФХз≥їйЗСе±Юз¶їе≠РпЉМдЊЛе¶В U^{3+} гАВдљЬдЄЇеЯЇиі®зЪДдЇЇеЈ•жЩґдљУдЄїи¶БжЬЙпЉЪеИЪзОЙпЉИ Al_{2}O_{3} пЉЙгАБйТЗйУЭзЯ≥ж¶ізЯ≥пЉИYttrium-aluminum-garnetпЉМYAGпЉЙгАБйТ®йЕЄйТЩпЉИ CaWO_{4} пЉЙгАБж∞ЯеМЦйТЩпЉИ GaF_{2} пЉЙгАБйУЭйЕЄйТЗпЉИ YAlO_{3} пЉЙеПКйУНйЕЄйХІпЉИ La_{2}Be_{2}O_{5} пЉЙз≠ЙгАВеЫЇдљУжњАеЕЙжЙАйЗЗзФ®зЪДзОїзТГдЄЇз°ЕйЕЄзЫРеЕЙе≠¶зОїзТГдЄОз£ЈйЕЄзЫРеЕЙе≠¶зОїзТГгАВињЩдЇЫжОЇжЭВеИ∞жЩґдљУжИЦзОїзТГдЄ≠зЪДйЗСе±Юз¶їе≠РпЉМеЕґдЄїи¶БзЙєзВєжШѓеЕЈжЬЙиЊГеЃљжЬЙжХИзЪДеРЄжФґеЕЙи∞±еЄ¶гАБйЂШиНІеЕЙжХИзОЗгАБиЊГйХњзЪДиНІеЕЙеѓњеСљеТМиЊГз™ДзЪДиНІеЕЙи∞±зЇњпЉМжШУдЇОдЇІзФЯеПЧжњАиЊРе∞ДгАВеЫЇдљУжњАеЕЙзЪДзІНз±їдЄОеЕґеЈ•дљЬж≥ҐйХње¶Ви°®4жЙАз§ЇпЉЪ

и°®4 еЫЇдљУжњАеЕЙзЪДзІНз±їдЄОеЕґеЈ•дљЬж≥ҐйХњ
вСҐеНКеѓЉдљУжњАеЕЙпЉЪ
еНКеѓЉдљУжњАеЕЙдљУзІѓе∞ПгАБжХИзЫКйЂШгАБжґИиАЧеКЯзОЗе∞ПгАБдљњзФ®еѓњеСљйХњпЉМеєґдЄФзФ±дЇОеНКеѓЉдљУP-NзїУзЪДзЙєжАІеЊИеЃєжШУзФ±зФµжµБе§Іе∞ПжЭ•и∞ГеИґеЕґиЊУеЗЇеКЯзОЗпЉМи∞ГеИґйҐСзОЗеПѓиЊЊGHzгАВеєњж≥ЫеЇФзФ®дЇОеЕЙзЇ§йАЪиЃѓгАБдњ°жБѓе§ДзРЖгАБеЃґзФµдЇІеУБдї•еПКз≤ЊеѓЖйЗПжµЛзЪДеЕ≥йФЃеЕГдїґгАВеНКеѓЉдљУжњАеЕЙжЭРжЦЩеПѓеИЖдЄЇеЕГзі†еНКеѓЉдљУеПКеМЦеРИзЙ©еНКеѓЉдљУгАВз°ЕдЄОйФЧеЕГзі†еНКеѓЉдљУжЭРжЦЩе±ЮдЇОйЧіжО•иГљйЪЩжЭРжЦЩпЉМдЄНиГљдљЬдЄЇеПСеЕЙжЭРжЦЩгАВеЄЄиІБзЪДеПСеЕЙеЕГдїґжЭРжЦЩе§ЪдЄЇзЫіжО•иГљйЪЩзЪДеМЦеРИзЙ©еНКеѓЉдљУпЉМе¶ВвЕҐжЧПгАБвЕ§жЧПзЪДз†ЈеМЦйХУдЄОз£ЈеМЦйУЯпЉМжИЦвЕ°жЧПгАБвЕ•жЧПзЪДз°ТеМЦйФМз≠ЙгАВдєЯеПѓдї•еИ©зФ®дЄЙеЕГжИЦеЫЫеЕГеМЦеРИзЙ©еНКеѓЉдљУпЉМе¶ВдЄЙеЕГеМЦеРИзЙ©еНКеѓЉдљУ Al_{x}Ga_{1-x}As жШѓдї•з†ЈеМЦйХУдЄОз†ЈеМЦйУЭжЙАеРИжИРпЉМи∞ГжХідЄЙдїЈеЕГзі† Al еТМ Ga зЪДжИРеИЖжѓФдЊЛдї•жФєеПШеЕґиГљйЪЩ E пЉМдїОиАМеЊЧеИ∞дЄНеРМж≥ҐйХњзЪДеЕЙпЉИ \lambda=1.24/EпЉИќЉmпЉЙ пЉЙгАВеНКеѓЉдљУжњАеЕЙзЪДзІНз±їдЄОеЕґеЈ•дљЬж≥ҐйХње¶Ви°®5жЙАз§ЇгАВ

и°®5 еНКеѓЉдљУжњАеЕЙзЪДзІНз±їдЄОеЕґеЈ•дљЬж≥ҐйХњ
вС£жґ≤дљУжњАеЕЙпЉЪ
жґ≤дљУжњАеЕЙеПИзІ∞жЬЙжЬЇжЯУжЦЩжњАеЕЙпЉИDye laserпЉЙпЉМе∞ЖдЄНеРМзЪДжЯУжЦЩзљЃдЇОжњАеЕЙеЕ±жМѓиЕФдЄ≠дљЬдЄЇжњАеЕЙжіїжАІдїЛиі®пЉМеЖНеИ©зФ®ж∞Ѓж∞ФжњАеЕЙгАБж∞©ж∞ФжњАеЕЙжИЦиАЕ Nd:YAG жњАеЕЙжЭ•иѓ±еѓЉжЬЙжЬЇжЯУжЦЩеПСеЕЙгАВжґ≤дљУйХ≠е∞ДеПѓдї•дЇІзФЯйЩ§XеЕЙе§ЦдїїдљХж≥ҐйХњзЪДжњАеЕЙпЉМжґ≤дљУжњАеЕЙжЙАзФ®зЪДжЯУжЦЩдїЛиі®дЄЇеЕЈжЬЙеЊИеЉЇеРЄжФґеЕЙи∞±иГљеКЫзЪДжЬЙжЬЇзЙ©иі®гАВзЫЃеЙНеПѓдљЬдЄЇжњАеЕЙжіїжАІдїЛиі®зЪДжЯУжЦЩзЇ¶жЬЙжХ∞зЩЊзІНпЉМеЈ•дљЬж≥ҐйХњеЬ®0.2-1ќЉmиМГеЫідєЛйЧігАВжѓПдЄАзІНжЯУжЦЩеПѓдї•еЬ®дЄАдЄ™еМЇеЯЯеЖЕжПРдЊЫињЮзї≠еПШеМЦзЪДеЈ•дљЬж≥ҐйХњпЉМеПѓеПШеМЦиМГеЫізЇ¶дЄЇ30-80nmпЉМе¶Ви°®6жЙАз§ЇдЄЇжґ≤дљУйХ≠е∞ДзІНз±їеПКеЕґж≥ҐйХњеПѓи∞ГиМГеЫігАВ

и°®6 жґ≤дљУйХ≠е∞ДзІНз±їеПКеЕґж≥ҐйХњеПѓи∞ГиМГеЫі
еЕЄеЮЛиДЙеЖ≤жЯУжЦЩжњАеЕЙзЪДзїУжЮДе¶ВеЫЊ38жЙАз§Ї[16]пЉМNd:YAGжњАеЕЙзїПињЗжЯ±зКґйАПйХЬиБЪзД¶жИРдЄАжЭ°зЇњиАМиОЈеЊЧжЮБйЂШзЪДж≥µжµ¶иГљйЗПеѓЖеЇ¶пЉМжњАеЕЙзЕІе∞ДеЬ®жЯУжЦЩзЫТеЖЕпЉМжЯУжЦЩеРЄжФґеЕЙи∞±иГљйЗПиАМеПСе∞ДиНІеЕЙпЉМдљњзФ®дЄНеРМжЯУжЦЩеН≥еПѓиОЈеЊЧдЄНеРМеЕЙи∞±еЄ¶зЪДиНІеЕЙпЉМеЬ®еЕ±жМѓиЕФзЪДдљЬзФ®дЄЛ嚥жИРжњАеЕЙйЬЗиН°гАВи∞ГжХіжЯУжЦЩжњАеЕЙз≥їзїЯеЖЕзЪДеЕЙж†ЕеИЩ嚥жИРжњАеЕЙж≥ҐйХњињЮзї≠еПѓи∞ГзЪДжњАеЕЙеЕЙжЇРпЉМеЫ†ж≠§жЯУжЦЩжњАеЕЙжЙАиЊУеЗЇеЕЙзЪДж≥ҐйХњдЄОеЕЙж†ЕиІТеЇ¶зЫЄеЕ≥гАВйАЪињЗдљњзФ®дЄНеРМзЪДжЯУжЦЩгАБдї•еПКйАЪињЗжЙЛеК®жИЦзФµиДСжОІеИґж≠•ињЫй©ђиЊЊжЭ•иЃЊеЃЪжЯУжЦЩжњАеЕЙеЕЙж†ЕзЇІжХ∞еТМеЕЙж†ЕиІТеЇ¶пЉМеН≥еПѓиОЈеЊЧзЙєеЃЪж≥ҐйХњзЪДжњАеЕЙиЊУеЗЇгАВ

еЫЊ38 иДЙеЖ≤жЯУжЦЩжњАеЕЙзЪДзїУжЮДз§ЇжДПеЫЊ
иЛ•йЬАи¶БжЫізЯ≠ж≥ҐйХњзЪДзіЂе§ЦеЕЙпЉМеИЩйЬАи¶БйАВељУйАЙзФ®жЩґдљУж≥ҐйХњеАНйҐСеЩ®пЉИwavelength extenderпЉЙпЉМдЇІзФЯиМГеЫі216-432nmзЪДеПѓи∞Гж≥ҐйХњзіЂе§ЦеЕЙгАВзФ±дЇОж≥ҐйХњеАНйҐСзЪДиЊУеЗЇиљђжНҐжХИзОЗжЬЙйЩРпЉИйАЪеЄЄдїЕдЄЇ10%пЉЙпЉМзїПињЗж≥ҐйХњеАНйҐСеРОзЪДеЕЙжЇРдЄ≠жЈЈеРИжЬЙеОЯжЬЙеЕЙжЇРдЄОеАНйҐСеРОзЪДзіЂе§ЦеЕЙжЇРпЉМеЫ†ж≠§йЬАи¶БзФ±ж£±йХЬе∞ЖеПѓиІБеЕЙеПКзіЂе§ЦеЕЙеИЖз¶їпЉМжЙНиГљеЊЧеИ∞жЙАйЬАи¶БзЪДзіЂе§ЦеЕЙгАВ
вС§еМЦе≠¶жњАеЕЙпЉЪ
еМЦе≠¶жњАеЕЙжШѓеИ©зФ®йЧ™еЕЙзБѓгАБзФµеЉІзБЂзД∞еК†зГ≠жИЦзЫіжО•еМЦе≠¶еПНеЇФжݕ胱僊嚥жИРжњАеЕЙгАВеМЦе≠¶жњАеЕЙзЪДзІНз±їеПКеЕґиЊУеЗЇж≥ҐйХње¶Ви°®7жЙАз§ЇгАВ

и°®7 еМЦе≠¶жњАеЕЙзЪДзІНз±їеПКеЕґиЊУеЗЇж≥ҐйХњ
вС•иЗ™зФ±зФµе≠РжњАеЕЙпЉИFree electron laserпЉЙпЉЪ
иЗ™зФ±зФµе≠РжњАеЕЙзЪДдЇІзФЯжЬЇеИґдЄОдЉ†зїЯжњАеЕЙдЄНеРМпЉМдЉ†зїЯжњАеЕЙеПЧйЩРдЇОжњАеЕЙеҐЮзЫКдїЛиі®жЭРжЦЩзЪДзЙєжАІпЉМйЪЊдї•дЇІзФЯињЬзЇҐе§ЦжИЦжЮБзЯ≠ж≥ҐйХњзЪДжњАеЕЙпЉЫиАМиЗ™зФ±зФµе≠РжњАеЕЙзЫіжО•дї•зФµе≠РжЭЯдЇІзФЯиЊРе∞ДгАБдЄНеАЯзФ®дїїдљХжњАеЕЙдїЛиі®пЉМжШѓзЫЃеЙНжЬАдљ≥зЪДињЬзЇҐе§ЦеПКзіЂе§ЦеЕЙйЂШеКЯзОЗжњАеЕЙеЕЙжЇРгАВеЕЄеЮЛиЗ™зФ±зФµе≠РжњАеЕЙеПѓжПРдЊЫеЈ•дљЬж≥ҐйХњзЇ¶248nm-8mmпЉМиДЙеЖ≤жЬАе§ІиЊУеЗЇеКЯзОЗеПѓиЊЊ1GWпЉМиЊУеЗЇж®°жАБдЄЇ TEM_{00} пЉМжЬАе§ІзЉЇзВєдЄЇдљУзІѓињЗе§ІгАВ
вС¶Xе∞ДзЇњжњАеЕЙпЉЪ
Xе∞ДзЇњжњАеЕЙдЄЇињСеєіжЭ•жЦ∞еПСе±ХзЪДжњАеЕЙеЕЙжЇРпЉМдЄїи¶БжШѓе∞ЖиДЙеЖ≤жњАеЕЙпЉИpulse laserпЉЙе∞ДеРСеЕЕжї°ж∞ФдљУзЪДзОїзТГзЃ°пЉМдљњзОїзТГзЃ°еЖЕж∞ФдљУжИРдЄЇжњАеПСжАБзЪДзФµжµЖпЉМеОЯе≠РеЖЕзЪДзФµе≠РиД±з¶їдЇІзФЯXе∞ДзЇњеЕЙе≠РпЉИX-ray photonпЉЙпЉМеЖНе∞ЖXе∞ДзЇњйАЪињЗеЕ±жМѓиЕФжФЊе§ІдЄАзЩЊиЗ≥дЄАеНГеАНпЉМеИґжИРеПѓеЗЭиБЪеЬ®дЄАиµЈзЪДXе∞ДзЇњеЕЙжЭЯгАВXе∞ДзЇњжњАеЕЙеЈ•дљЬж≥ҐйХњдЄЇ3.6-46.9nmпЉМжШѓдЊЭжНЃеЕґзОїзТГзЃ°еЖЕж∞ФдљУзФµжµЖзЪДжИРеИЖжЭ•еЖ≥еЃЪгАВе¶Ви°®8жЙАз§ЇдЄЇXе∞ДзЇњжњАеЕЙзЪДзІНз±їгАВ

и°®8 Xе∞ДзЇњжњАеЕЙзЪДзІНз±ї
еРДзІНйЫЈе∞ДеЕЙжЇРж≥ҐйХњдЄОдїЛиі®жЭРжЦЩзЪДжАІиі®еПѓеПВиАГMarvin J. WeberзЪДHandbook of Laser Wavelengths
жЬАеРОзФ®и°®9еѓєжѓФAOIеЄЄиІБеЕЙжЇРзЪДзЙєзВєпЉЪ

и°®9 AOIеЄЄиІБеЕЙжЇРзЪДзЙєзВє
дЄЙгАБиЙ≤ељ©дЄОйҐСи∞±
1.еК†иЙ≤жЈЈеРИдЄОеЗПиЙ≤жЈЈеРИ
йҐСи∞±жППињ∞еЃҐиІВзЪДзЙ©зРЖпЉМиЙ≤ељ©еИЩжШѓдЄїиІВжДЯеЃШжДЯеПЧгАВCIE1931йАЪињЗиЙ≤ељ©з©ЇйЧіжЭ•жППињ∞гАБеЃЪдєЙгАБи°°йЗПињЩзІНдЄїиІВжДЯиІЙпЉМжЬђзЂ†иКВиЃ≤ињ∞е¶ВдљХдљњзФ®дЄНеРМзЪДйҐЬиЙ≤и∞ГйЕНзїЩдЇЇзЫЄеЇФиЙ≤ељ©жДЯиІЙзЪДеЕЙгАВдЄїи¶БжЬЙдЄ§зІНжЦєеЉПпЉЪеК†иЙ≤ж≥ХдЄОеЗПиЙ≤ж≥ХгАВ
еК†иЙ≤жЈЈеРИжППињ∞зФ±дЄНеРМйҐЬиЙ≤зЪДеЕЙжЈЈеРИжИРжЦ∞йҐЬиЙ≤зЪДжГЕ嚥пЉМдЄЙзІНеК†иЙ≤еОЯиЙ≤дЄЇзЇҐиЙ≤гАБзїњиЙ≤еТМиУЭиЙ≤пЉЫзФµиДСжШЊз§ЇеЩ®еТМзФµиІЖжШѓеК†иЙ≤ж≥ХжЬАеЄЄиІБзЪД嚥еЉПпЉМиАМеЬ®ж≤єжЉЖгАБйҐЬжЦЩеТМељ©иЙ≤жї§еЕЙзЙЗз≠ЙеПНе∞ДжИЦйАПе∞ДеЕЙзЇњзЪДзЫЃж†ЗзЙ©иЙ≤ељ©еИЩдљњзФ®еЗПиЙ≤ж≥ХгАВеК†иЙ≤ж≥ХзЪДеПСжШОиАЕжШѓи©єеІЖжЦѓйЇ¶еЕЛжЦѓйЯ¶пЉМдїЦзЪДеП¶дЄАж۳襀дЄЦдЇЇжЙАзЯ•зЪДз†Фз©ґжИРжЮЬжШѓйЇ¶еЕЛжЦѓйЯ¶жЦєз®ЛзїДгАВ

еЫЊ39 еК†иЙ≤ж≥ХдЄЙеОЯиЙ≤
еЗПиЙ≤жЈЈеРИж®°еЮЛиІ£йЗКдЇЖжґВжЦЩгАБжЯУжЦЩгАБ奮ж∞іеТМ姩зДґиЙ≤зі†зЪДжЈЈеРИзЙ©дЇІзФЯзЪДйҐЬиЙ≤пЉМжѓПдЄ™йҐЬиЙ≤дЉЪеЗПеОїпЉИеН≥еРЄжФґпЉЙжЯРдЇЫж≥ҐйХњзЪДеЕЙеєґеРСеЕґдїЦеПНе∞ДгАВи°®йЭҐжЙАжШЊз§ЇзЪДйҐЬиЙ≤еПЦеЖ≥дЇОеЃГеПНжШ†еЬ®зФµз£Бж≥Ґи∞±зЪДйҐЬиЙ≤пЉЫжЙУеН∞жܯ奮ж∞ійҐЬиЙ≤жШѓеЗПиЙ≤ж≥ХжЬАеЄЄиІБзЪД嚥еЉПгАВеЗПиЙ≤ж≥ХдљњзФ®зЪДдЄЙзІНйҐЬиЙ≤дЄЇйїДиЙ≤гАБйЭТиЙ≤дї•еПКеУБзЇҐпЉМдЄОеК†иЙ≤ж≥ХзЫЄжѓФжИСдїђеПѓдї•еПСзО∞еЃГдїђеИЖеИЂжШѓзЇҐгАБзїњеЕЙпЉМзїњгАБиУЭеЕЙпЉМиУЭгАБзЇҐеЕЙжЈЈеРИиАМжИРзЪДйҐЬиЙ≤гАВ

еЫЊ40 еЗПиЙ≤ж≥ХдЄЙеОЯиЙ≤
2.жЉФиЙ≤жАІжМЗжХ∞ Color Rendering Index, CRI
дЄАиИђжГЕеЖµдЄЛиЃ§дЄЇпЉМдЇЇйА†еЕЙжЇРеЇФиЃ©дЇЇж≠£з°ЃеЬ∞жДЯзЯ•иЙ≤ељ©пЉМе∞±е¶ВеРМеܮ姙йШ≥еЕЙдЄЛзЬЛзЪДзЙ©еУБдЄАж†ЈгАВжЉФиЙ≤жАІжМЗжХ∞пЉИCRIпЉЙдЄЇзЙ©еУБеЬ®дЄАдЄ™зЕІжШОеЕЙжЇРдЄЛжШЊз§ЇзЪДйҐЬиЙ≤дЄОиѓ•зЙ©еУБеЬ®еПВзЕІеЕЙжЇРзЕІе∞ДдЄЛпЉМдЄ§зІНжГЕеЖµдЇЇз±їжДЯзЯ•йҐЬиЙ≤зЪДзЫЄеѓєеЈЃеЉВеПВжХ∞гАВеЫљйЩЕзЕІжШОеІФеСШдЉЪпЉИCIEпЉЙеѓєеЕґеЃЪдєЙдЄЇпЉЪ
жЉФиЙ≤жАІпЉЪеЕЙжЇРеѓєзЙ©дљУйА†жИРзЪДйҐЬиЙ≤жХИжЮЬзЫЄиЊГдЇОеПВиАГеЕЙжЇРзЪДзЙєжАІпЉМзФ±жЬЙжДПиѓЖжИЦжЧ†жДПиѓЖзЪДиІВеѓЯеЊЧеЗЇгАВ CRIжШѓеѓєдЇОзЕІжШОеЕЙжЇРзЙєжАІињЫи°Мж†ЗеЃЪзЪДеПВжХ∞гАВCRIжХ∞еАЉиѓДеЃЪж≥Хе∞ЖеЊЕжµЛеЕЙжЇРдЄОеПВзЕІеЕЙжЇРпЉМеЬ®DIN 6169жЙАиІДеЃЪзЪДзЪДеЕЂдЄ™иЙ≤ж†ЈдЄКйАРдЄАдљЬжѓФиЊГеєґйЗПеМЦеЕґеЈЃеЉВжАІпЉМеЈЃеЉВжАІиґКе∞ПеИЩдї£и°®еЊЕжµЛеЕЙжЇРзЪДжЉФиЙ≤жАІиґКе•љгАВдЄАдЄ™еЕЙжЇРзЪДжЉФиЙ≤жАІжМЗжХ∞CRIпЉМдЄНзЫіжО•и°®зО∞дЄАдЄ™еЕЙжЇРзЪДйҐЬиЙ≤гАВжЉФиЙ≤жАІеПЦеЖ≥дЇОеЕЙжЇРзЪДеЕЙи∞±пЉМељУеЕЙжЇРзЪДеЕЙи∞±жґµзЫЦж≥ҐйХњиґКеєњпЉМеИЩиѓ•еЕЙжЇРзЪДжЉФиЙ≤жАІжМЗжХ∞иґКйЂШгАВдЊЛе¶ВзЩљзВљзБѓжЛ•жЬЙињЮзї≠зЪДеЕЙи∞±пЉМиАМLEDгАБHIDеИЩжШѓз¶їжХ£зЪДзЇњеЕЙи∞±пЉМеЫ†ж≠§зЩљзВљзБѓзЪДCRIжМЗжХ∞жѓФLEDгАБHIDи¶БйЂШпЉМе¶ВеЫЊ41жЙАз§ЇгАВ

еЫЊ41 дЄНеРМеЕЙжЇРCRIжѓФиЊГ
CRIдЄОиЙ≤жЄ©зЫЄзїУеРИжШѓжѓФиЊГдЄНеРМеЕЙжЇРдєЛйЧізЪДжЬАдљ≥жЦєеЉПгАВдЄАдЄ™еЄЄиІБзЪДиѓѓеМЇжШѓиЙ≤жЄ©еТМCRIйГљжППињ∞дЇЖзБѓзЪДзЫЄеРМе±ЮжАІпЉЪиЙ≤жЄ©жППињ∞дЇЖеЕЙжЇРзЪДе§ЦиІВйҐЬиЙ≤пЉМCRIжППињ∞дЇЖеЕЙзЇњеЬ®еРДзІНзЙ©дљУдЄ≠еСИзО∞йҐЬиЙ≤зЪДз®ЛеЇ¶гАВи¶БжѓФиЊГдїїдљХдЄ§дЄ™зїЩеЃЪеЕЙжЇРзЪДCRIз≠ЙзЇІпЉМеЃГдїђењЕй°їеЕЈжЬЙзЫЄеРМзЪДиЙ≤жЄ©жЙНиГљдљњжѓФиЊГеЕЈжЬЙдїїдљХжДПдєЙгАВ
3.еЖЈиЙ≤дЄОжЪЦиЙ≤
дЄОйїСдљУиЊРе∞ДжЙАеЃЪдєЙзЪДиЙ≤жЄ©дЄНеРМпЉМеЖЈиЙ≤дЄОжЪЦиЙ≤жШѓеЯЇдЇОдЇЇз±їиЙ≤ељ©иЃ§зЯ•еЃЪдєЙзЪДгАВеЖЈжЪЦиЙ≤и∞ГжМЗиЙ≤ељ©ењГзРЖдЄКзЪДеЖЈзГ≠жДЯиІЙпЉМжККйҐЬиЙ≤еИЖз±їдЄЇжЪЦиЙ≤и∞ГпЉИзЇҐгАБж©ЩгАБйїДгАБж£ХпЉЙгАБеЖЈиЙ≤и∞ГпЉИзїњгАБйЭТгАБиУЭгАБзіЂпЉЙеТМдЄ≠иЙ≤и∞ГпЉИйїСгАБзЩљгАБзБ∞пЉЙдЄЙзІНпЉМе¶ВеЫЊ42жЙАз§ЇгАВ

еЫЊ42 еЖЈжЪЦиЙ≤и∞Г
еЖНжђ°еЉЇи∞ГпЉЪиЙ≤жЄ©жШѓзФ±йїСдљУиЊРе∞ДзЪДзГ≠еКЫе≠¶жЄ©еЇ¶еЃЪдєЙзЪДпЉМжШѓдЄАдЄ™зЙ©зРЖж¶ВењµпЉЫеЖЈжЪЦиЙ≤и∞ГжШѓеЯЇдЇОдЇЇз±їиЙ≤ељ©иЃ§зЯ•еЃЪдєЙзЪДпЉМжШѓдЄАдЄ™ењГзРЖе≠¶ж¶ВењµгАВ
еЫЫгАБеЕЙжЇРдЄОжСДељ±жЬЇ
1.жДЯеЕЙеЕГдїґзЪДеЕЙи∞±жХПжДЯеЇ¶
еЬ®дЇЇз±їиІЖиІЙдЄ≠пЉМзЬЉзЭЫиІЖзљСиЖЬзЪДеРДзІНиІЖиІЙзїЖиГЮеЬ®ињЮзї≠еЕЙи∞±дЄЛпЉМеѓєдЄНеРМж≥ҐйХњзЪДеЕЙеЕЈжЬЙдЄНеРМз®ЛеЇ¶зЪДжХПжДЯеЇ¶гАВеЕЙзЇњдљЬзФ®дЇОиІЖйФ•зїЖиГЮе§ЦжЃµпЉМдїЦдїђзЪДе§ЦжЃµзїЖиГЮиЖЬдЉЪдЇІзФЯзФµдљНпЉМеЃМжИРеЕЙ-зФµжНҐиГљзЪДзђђдЄАж≠•гАВдЇЇйА†зЪДеЕЙжДЯжµЛеЩ®пЉМеН≥зЫЄжЬЇз≠ЙиЃЊе§ЗзЪДж†ЄењГжДЯеЕЙеЕГдїґпЉМ襀职聰жЬЙз±їдЉЉзЪДеКЯиГљгАВзО∞дїКзФµиНЈиА¶еРИеЕГдїґпЉИCharge-coupled DeviceпЉМCDDпЉЙдЄОдЇТи°•жАІж∞ІеМЦйЗСе±ЮеНКеѓЉдљУпЉИComplementary Metal-oxide SemiconductorпЉМCMOSпЉЙжДЯжµЛеЩ®жШѓеПЦеГПз≥їзїЯдЄ≠жЬАеЄЄдљњзФ®зЪДеЕЙжДЯжµЛеЩ®пЉМзљЃдЇОеЕЙе≠¶з≥їзїЯзЪДзД¶еє≥йЭҐдєЛдЄКгАВйАЪеЄЄжШѓдЄАзїДеѓєеЕЙеПѓжДЯеЇФзЪДеНХдљНпЉМеПИзІ∞еГПзі†пЉИpixelпЉЙпЉМзїДжИРдЄАзїіжИЦдЇМзїізЪДйШµеИЧпЉМе∞ЖеЕЙиЊРе∞ДзЪДиГљйЗПиљђжНҐжИРзФµиНЈгАВиАМељ±еУНжДЯжµЛеЩ®зЪДеУБиі®дЄОеЕґзЫЄеЕ≥зФµиЈѓзЪДиЃЊиЃ°пЉМеѓєжХідЄ™еПЦеГПз≥їзїЯзЪДжХИиГљжЬЙжЮБе§Іељ±еУНгАВ
еѓєдЇОCCDжИЦCMOSзЪДеЕЙжДЯжµЛеЩ®пЉМеЕґеПЧеЕЙи°®йЭҐжФґеИ∞зЪДеЕЙе≠Ре∞ЖдЉЪиљђжНҐдЄЇеЕЙзФЯзФµе≠РпЉМињЫиАМдЇІзФЯзЫЄеЇФеЉЇеЇ¶зЪДзФµдњ°еПЈгАВеѓєдЇОиѓ•жДЯжµЛеЩ®иГље§ЯдЇІзФЯеЕЙзФЯзФµе≠РзЪДиГљеКЫпЉМжИСдїђзФ®йЗПе≠РжХИзОЗпЉИQuantum efficiencyпЉЙжЭ•еѓєеЕЙжХПжЬЯйЧізЪДеЕЙжХПжДЯжАІињЫи°Мз≤Њз°ЃзЪДйЗПжµЛгАВйЗПе≠РжХИзОЗзЪДеЃЪдєЙпЉЪ
QE=\frac{Electrons/sec}{Photons/sec}=\frac{current/charge\ of\ 1\ electron}{(total\ power\ of\ photons)/(energy\ of 1\ photon)}\\йЗПе≠РжХИзОЗ=\frac{еНХдљНжЧґйЧіеЖЕдЇІзФЯзЪДеЕЙзФЯзФµе≠РжХ∞}{еНХдљНжЧґйЧіеЖЕзЪДеЕ•е∞ДеЕЙе≠РжХ∞}\\ зФ±дЇОеЕЙе≠РзЪДиГљйЗПдЄОж≥ҐйХњзЪДеАТжХ∞жИРжѓФдЊЛпЉМеЫ†ж≠§йЗПе≠РжХИзОЗзЪДйЗПжµЛйАЪеЄЄжШѓеЬ®дЄАжЃµж≥ҐйХњиМГеЫіеЖЕињЫйЗПжµЛгАВе¶ВеЫЊ43жЙАз§ЇпЉМдЄЇеУИеЛГжЬЫињЬйХЬжЙАйЕНе§ЗзЕІзЫЄжЬЇзЪДжДЯеЕЙиА¶еРИеЕГдїґеѓєдЄНеРМж≥ҐйХњеЕЙдњ°еПЈзЪДйЗПе≠РжХИзОЗжЫ≤зЇњеЫЊпЉЪ

еЫЊ43 еУИеЛГжЬЫињЬйХЬжЙАйЕНе§ЗзЕІзЫЄжЬЇзЪДжДЯеЕЙиА¶еРИеЕГдїґеѓєдЄНеРМж≥ҐйХњеЕЙдњ°еПЈзЪДйЗПе≠РжХИзОЗжЫ≤зЇњеЫЊ
еРМж†ЈжШѓеНХдљНжЧґйЧіеЖЕ100дЄ™еЕЙе≠РеЕ•е∞ДеЬ®дЄАдЄ™еГПзі†еНХдљНдЄКпЉМQE=70%жДПеС≥зЭАзЫЄжЬЇзЪДеЕЙжДЯжµЛеЩ®иГље§ЯиљђжНҐеЊЧеИ∞70дЄ™зФµе≠РпЉЫQE=30%жДПеС≥зЭАеП™иГљеЊЧеИ∞30дЄ™зФµе≠РгАВжШЊзДґйЗПе≠РжХИзОЗиґКйЂШзЫЄжЬЇжЙАиГљжО•жФґеИ∞зЪДжЬЙжХИдњ°жБѓиГљйЗПиґКе§ІпЉМеѓєдЇОзЫЄеРМеЉЇеЇ¶зЪДиГМжЩѓеЩ™е£∞пЉМеЕґдњ°еЩ™жѓФиґКйЂШгАВ
еЕ≥дЇОзЫЄжЬЇзЪДQEпЉМзЬЛеРДе§ІеОВеХЖжПРдЊЫзЪДдЇІеУБиµДжЦЩпЉИdatasheetпЉЙжЧґењЕй°їзЙєеИЂж≥®жДПдї•дЄЛдЄ§зВєпЉЪ
- йЗПе≠РжХИзОЗжШѓдЄОж≥ҐйХњзЫЄеЕ≥зЪДпЉМеРМдЄАеП∞зЫЄжЬЇгАБдЄНеРМж≥ҐйХњзЪДйЗПе≠РжХИзОЗеєґдЄНзЫЄеРМпЉМеЫ†ж≠§жИСдїђйЬАи¶БжЯ•зЬЛе¶ВеЫЊ43зЪДињЩзІНйЗПе≠РжХИзОЗжЫ≤зЇњеЫЊпЉМжШОз°Ѓз≥їзїЯжЙАдљњзФ®еЕЙжЇРзЪДж≥ҐйХњж≥ҐжЃµе§Диѓ•зЫЄжЬЇзЪДйЗПе≠РжХИзОЗи°®зО∞
- йАЪеЄЄеЬ®йЂШзЂѓзІСз†ФзЫЄжЬЇзЪДеПВжХ∞и°®дЄ≠жЙАзЬЛеИ∞зЪДйАЪеЄЄжШѓйЗПе≠РжХИзОЗзЪДе≥∞еАЉпЉМдєЯе∞±жШѓзЫЄжЬЇжЬАзБµжХПж≥ҐйХњжЙАеѓєеЇФзЪДйЗПе≠РжХИзОЗгАВзЫЄеЇФзЪДпЉМеЕґеПВжХ∞и°®дЄ≠жЙАеИЧдЄЊзЪДжЬАе§Ідњ°еЩ™жѓФпЉИMax. SNRпЉЙдєЯжШѓеЬ®жЬАйЂШйЗПе≠РжХИзОЗзЪДж≥ҐйХњдЄЛгАБзїУеРИеЕґдїЦзРЖжГ≥зЪДеЕЙзЕІжЭ°дїґеБЪеЗЇжЭ•зЪДдЉШзІАжХ∞жНЃпЉИдєЯеЫ†ж≠§ињЩдЄ™жЬАе§Ідњ°еЩ™жѓФеЃЮдЄЇеЇЯиѓЭдЄАжЃµпЉЙгАВдЄНеРМзЫЄжЬЇжДЯеЕЙеЕГдїґзЪДйЗПе≠РжХИзОЗе≥∞еАЉеѓєеЇФзЪДж≥ҐйХњеРДдЄНзЫЄеРМпЉМеЫ†ж≠§жЬАе•љиГље§ЯйАЪињЗйЗПе≠РжХИзОЗжЫ≤зЇњеОїеМєйЕНз≥їзїЯеЕЙжЇРж≥ҐйХњжЭ•иѓДдЉ∞иѓ•зЫЄжЬЇеЬ®жЬђз≥їзїЯдЄ≠зЪДйЗПе≠РжХИзОЗи°®зО∞гАВ
е¶ВеЫЊ44пЉМдЄЇFLIRзЪДдЄАжђЊеБПжМѓжАБзЫЄжЬЇBFS-U3-51S5PпЉМжР≠иљљSONYзЪДеБПжМѓжАБCMOSпЉИPCMOSпЉЙпЉМ襀зФ®дЇОењЂйАЯз©ЇйЧізЫЄзІїжЬѓдЄ≠пЉИдЄАжђ°жИРеГПеН≥еПѓеЃМжИРеЫЫж≠•зЫЄзІїжЬѓпЉЙгАВ

еЫЊ44 BFS-U3-51S5PеБПжМѓжАБзЫЄжЬЇ
ињЩжШѓдЄАжђЊеНХиЙ≤зЫЄжЬЇпЉИmono typeпЉЙпЉМеЕґйЗПе≠РжХИзОЗжЫ≤зЇње¶ВеЫЊ45жЙАз§ЇпЉЪ

еЫЊ45 BFS-U3-51S5PеБПжМѓжАБзЫЄжЬЇйЗПе≠РжХИзОЗжЫ≤зЇњ
иЩЪзЇње§ДдЄЇ530nmпЉИзїњеЕЙпЉЙеЕЙзЇњдЄЛиѓ•зЫЄжЬЇеЕЙжДЯжµЛеЩ®зЪДйЗПе≠РжХИзОЗпЉЪ21.0461%гАВ
иАМеѓєдЇОељ©иЙ≤зЫЄжЬЇпЉИcolor typeпЉЙпЉМеИЩйЬАи¶БйТИеѓєзЫЄжЬЇжДЯеЕЙеЕГдїґдЄКдЄЙзІНдЄНеРМж≥ҐжЃµзЪДжДЯжµЛеГПзі†жµЛеЃЪйЗПе≠РжХИзОЗжЫ≤зЇњгАВе¶ВеЫЊ46пЉМдЄЇеЊЈеЫљiDSзЪДUI-3590CP-HQзЫЄжЬЇпЉМеЕґжДЯжµЛеЩ®дЄЇзО∞дїКпЉИ2022еєіпЉЙеГПзі†е§Іе∞ПжЬАе∞ПзЪДзЫЄжЬЇгАВ

еЫЊ46 iDS UI-3590CP-HQзЫЄжЬЇ
ињЩжШѓдЄАжђЊељ©иЙ≤зЫЄжЬЇпЉМеЕґдЄЙзІНжДЯеЕЙеГПзі†зЪДйЗПе≠РжХИзОЗжЫ≤зЇње¶ВеЫЊ47жЙАз§ЇпЉЪ

еЫЊ47 iDS UI-3590CP-HQзЫЄжЬЇйЗПе≠РжХИзОЗжЫ≤зЇњ
зЫЄиЊГдЇОзЫЄжЬЇеОВеХЖжПРдЊЫзЪДжЙАи∞УжЬАе§Ідњ°еЩ™жѓФеПВжХ∞пЉМйЗПе≠РжХИзОЗжЫ≤зЇњиГљиЊГе§Із®ЛеЇ¶зЪДдЊІйЭҐеПНеЇФиѓ•жђЊзЫЄжЬЇеЬ®дЄНеРМж≥ҐйХњдЄЛзЪДдњ°еЩ™и°®зО∞пЉМдљЖжШѓеѓєдЇОе§Іе§ЪжХ∞еОВеХЖжЭ•иѓіпЉМйЗПе≠РжХИзОЗжЫ≤зЇњйÚ襀иЧПеЬ®еЗ†еНБдЄКзЩЊй°µзЪДдЇІеУБжЙЛеЖМпЉИHandbookпЉЙдєЛдЄ≠пЉМзФЪиЗ≥йЬАи¶БжЙЊзЫЄжЬЇжЙАдљњзФ®зЪДеЕЙжДЯжµЛеЩ®еОВеХЖзЪДдЇІеУБжЙЛеЖМжЙНиГљжЙЊеИ∞йЗПе≠РжХИзОЗиµДжЦЩгАВеЊИе§ЪзЫЄжЬЇеОВеХЖзЪДдЇІеУБзЃАдїЛдЄ≠еєґдЄНдЉЪзЫіжО•жФЊеЗЇйЗПе≠РжХИзОЗжЫ≤зЇњгАВ
2.зЩљеє≥и°°
зЩљеє≥и°°пЉИWhite balanceпЉЙпЉМеЕґеЯЇжЬђж¶ВењµдЄЇвАЬдЄНзЃ°еЬ®дїїдљХеЕЙжЇРдЄЛпЉМйГљиГље∞ЖзЩљиЙ≤зЙ©дљУињШеОЯдЄЇзЩљиЙ≤вАЭпЉМеѓєеЬ®зЙєеЃЪеЕЙжЇРдЄЛжЛНжСДдЇІзФЯзЪДеБПиЙ≤зО∞и±°пЉМйАЪињЗеК†еЉЇзЫЄеЇФзЪДи°•иЙ≤жЭ•ињЫи°Ми°•еБњгАВзЫЄжЬЇзЪДзЩљеє≥и°°иЃЊеЃЪзФ®дЇОж†°еЗЖиЙ≤жЄ©зЪДеБПеЈЃпЉМеЬ®жЛНжСДжЧґйАЪињЗи∞ГжХізЫЄжЬЇзЪДзЩљеє≥и°°жЭ•иОЈеЊЧзЫЄеЇФзЪДзФїйЭҐжХИжЮЬгАВе¶ВеЫЊ48дЄЇдЄНеРМиЙ≤жЄ©зЪДеЕЙзЇњзЕІжШОпЉМзЩљеє≥и°°зЪДи∞ГжХіе∞±еПѓдї•ж†єжНЃдЄНеРМиЙ≤жЄ©дЄЛзЪДзЩљиЙ≤пЉМж†°ж≠£зЫЄеЇФзЪДRGBжѓФдЊЛпЉМ嚥жИРе¶ВеЫЊ49зЪДзФїйЭҐжХИжЮЬгАВ

еЫЊ48 дЄНеРМиЙ≤жЄ©дЄЛзЪДзЩљиЙ≤

еЫЊ49 дЄНеРМзЩљеє≥и°°дЄЛжЛНжСДзЪДзЕІзЙЗ
зЩљеє≥и°°зЪДи∞ГжХіеПѓдї•еЬ®дЄАеЃЪиМГеЫіеЖЕжПРеНЗдїОзЕІзЙЗдЄ≠зЪДзїЖиКВгАВйТИеѓєзЫЄеЇФзЪДзЕІжШОеЕЙиЙ≤жЄ©пЉМдЊЛе¶ВйТ®дЄЭзБѓ3200KеЈ¶еП≥пЉМеПѓдї•зЬЛеИ∞е¶ВеЫЊ50еЈ¶еЫЊпЉМжЬ™зїПзЩљеє≥и°°и∞ГжХізЪДеЫЊзЙЗдЄКзМ™жОТдЄКзЪДеТЦеЦ±дЄОзМ™жОТйҐЬиЙ≤жЧ†ж≥ХеМЇеИЖгАВељУзЫЄжЬЇиЃЊеЃЪзЩљеє≥и°°еЬ®3200KжЧґпЉМзЫЄжЬЇеЖЕзљЃзЪДзЃЧж≥ХдЉЪйТИеѓєињЩдЄАиЙ≤жЄ©ињЫи°МиЗ™еК®и°•иЙ≤пЉМе¶ВеЫЊ5еП≥еЫЊпЉМзїПињЗзЩљеє≥и°°и°•иЙ≤еРОеПѓдї•еМЇеИЖеЗЇзМ™жОТеТМзМ™жОТдЄКзЪДеТЦеЦ±зЪДйҐЬиЙ≤дєЛеИЖгАВ

еЫЊ50 еЈ¶еЫЊжЬ™и∞ГжХізЩљеє≥и°°пЉМеП≥еЫЊи∞ГжХізЩљеє≥и°°дЄЇ3200KдєЛеРО
дЇФгАБеЕЙжЇРдЄОеЊЕжµЛзЙ©
1.жШОдЄОжЪЧ
жШОжЪЧпЉМеЬ®зЊОжЬѓдЄ≠еПИзІ∞дЄЇжШОжЪЧи∞Ге≠РпЉМжШѓжМЗзЙ©дљУеПЧеЕЙгАБиГМеЕЙйГ®еИЖзЪДжШОжЪЧеПШеМЦпЉМеЬ®зЙ©дљУдЇОеЕЙжЇРзЕІе∞ДдЄЛпЉМзЙ©дљУеСИзО∞еЗЇжШОжЪЧдЄ§зІНзКґжАБпЉМеЬ®дЇЃйЭҐдЄОжЪЧйЭҐдєЛйЧіпЉМе≠ШеЬ®зФ±дЇОзЙ©дљУе§Ци°®зЪД嚥зКґгАБеЕЙжЇР嚥зКґз≠ЙеѓЉиЗізЪДжЄРе±ВеИЖеЄГгАВйАЪеЄЄдЄАдЄ™зЙ©дљУеЬ®еЕЙжЇРзЕІе∞ДдЄЛзЪДжШОжЪЧеИЖеЄГеПѓдї•ељТзЇ≥дЄЇе¶ВеЫЊ51зЪД5дЄ™зїДжИРйГ®еИЖпЉЪ
- жЄРжЩХShading
- Attached ShadowпЉИжЬ™жЙЊеИ∞еРИйАВзЪДдЄ≠жЦЗиѓСеРНпЉМеЕґеРЂдєЙжШѓзЙ©дљУи°®йЭҐдЄКзЪДељ±е≠РпЉМеМЇеИЖдЇОзЙ©дљУжКХељ±еЬ®еЕґдїЦзЙ©дљУзЪДељ±е≠РпЉЙ
- еПНеЕЙInter-reflection
- жКХељ±Cast Shadow
- еНКељ±Penumbra

еЫЊ51
2.йШіељ±зЪДжЄРжЩХ
йШіељ±зЪДжЄРжЩХзФ±еЕЙжЇРзЪД嚥зКґдЇІзФЯгАВдЊЛе¶Ве¶ВеЫЊ52жЙАз§ЇзЪДзРЖжГ≥зВєеЕЙжЇРпЉМеЫ†дЄЇеЕЙж≤њзЫізЇњдЉ†жТ≠пЉМдЇОеҐЩйЭҐдЄК嚥жИРзЪДељ±е≠РпЉМдЇЃдЄОжЪЧдєЛйЧідЇ§жО•еИЖжШОгАВ

еЫЊ52
зДґиАМеЃЮйЩЕдЄКеЕЙжЇРдЄНеПѓиГљдЄЇдЄАдЄ™зВєпЉМзЫЄеѓєдЇОжКХељ±зЪДиІЖиІТеЕЙжЇРдЄАеЃЪдЉЪжШѓдЄАдЄ™йЭҐпЉМињЩдЄ™йЭҐзІѓеПѓдї•йЭЮеЄЄе∞ПпЉМдљЖињШжШѓдЄАдЄ™йЭҐгАВдЇОжШѓе¶ВеЫЊ53жЙАз§ЇпЉМеРМж†ЈеЯЇдЇОеЕЙж≤њзЫізЇњдЉ†жТ≠пЉМзФ±дЇОеЕЙжЇРе≠ШеЬ®йЭҐзІѓпЉМжКХељ±еЬ®еҐЩдЄКзЪДжШОжЪЧдЇ§зХМе§ДзФ±дЇОдЄНеРМдљНзљЃиÚ襀дЄНеРМйЭҐзІѓе§Іе∞ПзЪДеЕЙжЇРжЙАзЕІе∞ДеИ∞пЉМеЫ†ж≠§дЇІзФЯжЄРжЩХе±Вжђ°гАВ

еЫЊ53
еЕ≠гАБеЕЙжЇРдЄОжї§еЕЙзЙЗ
1.жї§еЕЙзЙЗзЪДеОЯзРЖ
жї§еЕЙзЙЗжШѓзФ®жЭ•йАЙеПЦжЙАйЬАзФµз£БиЊРе∞Дж≥ҐжЃµзЪДеЕЙе≠¶еЩ®дїґгАВеЕґеЈ•дљЬеОЯзРЖе∞±жШѓеРЄжФґжИЦеПНе∞ДзїЭе§ІйГ®еИЖж≥ҐйХњпЉМеП™еЕБиЃЄзЙєеЃЪж≥ҐйХњзїДеИЖзЪДзФµз£БиЊРе∞ДйАПе∞ДгАВжї§еЕЙзЙЗйАЪеЄЄжШѓе°СжЦЩжИЦиАЕзОїзТГзЙЗдљЬдЄЇеЯЇжЭРпЉМеЖНеК†еЕ•зЙєзІНжЯУжЦЩеИґжИРгАВ
еєњдєЙдЄКзЪДжї§еЕЙзЙЗеПѓеИЖдЄЇдЄ§е§Із±їпЉЪеРЄжФґеЉПжї§еЕЙзЙЗпЉИAbsorptive FilterпЉЙеТМдЇМеРСиЙ≤жї§еЕЙзЙЗпЉИDichroic FilterпЉЙгАВдЄ§иАЕзЪДеМЇеИЂдЄНеЬ®дЇОињЗжї§зЪДзФµз£БиЊРе∞ДзІНз±їпЉМиАМеЬ®дЇОињЗжї§жЦєеЉПгАВеЬ®еРЄжФґеЉПжї§еЕЙзЙЗдЄ≠пЉМеЕЙдЉЪж†єжНЃжЙАзФ®зОїзТГеЯЇжЭњзЪДеРЄжФґзЙєжАІиАМ襀йШїжМ°гАВжНҐеП•иѓЭиѓіпЉМ襀йШїжМ°зЪДеЕЙдЄНдЉЪ襀濧еЕЙзЙЗеПНе∞ДпЉМиАМж؃襀еРЄжФґеєґеМЕеРЂеЬ®ињЗжї§еЩ®дЄ≠гАВеѓєдЇОз≥їзїЯдЄ≠жґИйЩ§зФ±жЭВжХ£еЕЙйА†жИРзЪДжЭВиЃѓпЉМеРЄжФґеЉПжї§еЕЙзЙЗжШѓзРЖжГ≥зЪДйАЙжЛ©гАВеРЄжФґеЉПжї§еЕЙзЙЗињШжЬЙдЄАдЄ™йҐЭе§ЦзЪДе•ље§ДжШѓиІТеЇ¶жХПжДЯеЇ¶дљОгАВеЕЙеПѓдї•дїОеЊИеЃљиМГеЫізЪДиІТеЇ¶еЕ•е∞ДеИ∞жї§еЕЙзЙЗдЄКпЉМжї§еЕЙзЙЗе∞ЖдњЭжМБеЕґйАПе∞ДеТМеРЄжФґзЙєжАІгАВ
дЇМеРСиЙ≤жї§еЕЙзЙЗзЪДеЈ•дљЬеОЯзРЖжШѓеПНе∞ДдЄНйЬАи¶БзЪДж≥ҐйХњпЉМеРМжЧґйАПе∞ДеЕЙи∞±зЪДжЙАйЬАйГ®еИЖгАВеЬ®жЯРдЇЫеЇФзФ®дЄ≠пЉМињЩжШѓдЄАзІНзРЖжГ≥зЪДжХИжЮЬпЉМеЫ†дЄЇеЕЙеПѓдї•жМЙж≥ҐйХњеИЖжИРдЄ§дЄ™еЕЙжЇРгАВињЩжШѓйАЪињЗжЈїеК†дЄАе±ВжИЦе§Ъе±ВдЄНеРМжКШе∞ДзОЗзЪДжЭРжЦЩжЭ•еИ©зФ®еЕЙж≥ҐзЪДеє≤жґЙзЙєжАІжЭ•еЃЮзО∞зЪДгАВеЬ®еє≤жґЙжї§еЕЙзЙЗдЄ≠пЉМдїОдљОжКШе∞ДзОЗжЭРжЦЩдЉ†жТ≠зЪДеЕЙдЉЪ襀йЂШжКШе∞ДзОЗжЭРжЦЩеПНе∞ДпЉЫеП™жЬЙзЙєеЃЪиІТеЇ¶еТМж≥ҐйХњзЪДеЕЙдЉЪзЫЄйХњеє≤жґЙеЕ•е∞ДеЕЙжЭЯеєґз©њињЗжЭРжЦЩпЉМиАМжЙАжЬЙеЕґдїЦеЕЙдЉЪзЫЄжґИеє≤жґЙеєґдїОжЭРжЦЩеПНе∞ДпЉИеЫЊ54пЉЙгАВ

еЫЊ54 дЇМеРСиЙ≤жї§еЕЙзЙЗз§ЇжДПеЫЊ
дЄОеРЄжФґжї§еЕЙзЙЗдЄНеРМпЉМдЇМеРСиЙ≤жї§еЕЙзЙЗеѓєеЕЙзЇњеЕ•е∞ДиІТеЇ¶жЮБдЄЇжХПжДЯгАВељУзФ®дЇОиґЕеЗЇеЕґйҐДжЬЯиЃЊиЃ°зЪДдїїдљХиІТеЇ¶жЧґпЉМдЇМеРСиЙ≤жї§еЕЙзЙЗжЧ†ж≥Хжї°иґ≥жЬАеИЭжМЗеЃЪзЪДйАПе∞ДзОЗеТМж≥ҐйХњиІДж†ЉгАВж†єжНЃзїПй™МпЉМйАЪињЗдЇМеРСиЙ≤жї§еЕЙзЙЗеҐЮеК†еЕ•е∞ДиІТдЉЪе∞ЖйАПе∞ДеЕЙзЇњзІїеРСжЫізЯ≠зЪДж≥ҐйХњпЉИеН≥жЫіиУЭзЪДж≥ҐйХњпЉЙпЉЫеЗПе∞ПиІТеЇ¶дЉЪе∞ЖйАПе∞ДеЕЙзЇњзІїеРСжЫійХњзЪДж≥ҐйХњпЉИеН≥жЬЭеРСжЫізЇҐзЪДж≥ҐйХњпЉЙ
жї§еЕЙзЙЗеЄЄзФ®дЇОжШЊеЊЃйХЬгАБеЕЙи∞±е≠¶гАБеМЦе≠¶еИЖжЮРеТМжЬЇеЩ®иІЖиІЙпЉМйАЪеЄЄжЬЙе§ЪзІНжї§еЕЙзЙЗз±їеЮЛеТМз≤ЊеЇ¶з≠ЙзЇІеПѓдЊЫйАЙжЛ©гАВжї§еЕЙзЙЗдЄїи¶БжЬЙдї•дЄЛеЕ≥йФЃжМЗж†ЗпЉЪ
дЄ≠ењГж≥ҐйХњ
зФ®дЇОеЃЪдєЙеЄ¶йАЪжї§ж≥ҐеЩ®зЪДдЄ≠ењГж≥ҐйХњпЉИCenter WavelengthпЉМCWLпЉЙжППињ∞дЇЖжї§еЕЙзЙЗдЉ†иЊУзЪДеЕЙи∞±еЄ¶еЃљзЪДдЄ≠зВєгАВдЉ†зїЯзЪДйХАиЖЬжї§еЕЙзЙЗпЉИCoated Optical FiltersпЉЙеАЊеРСдЇОеЬ®дЄ≠ењГж≥ҐйХњйЩДињСеЃЮзО∞жЬАе§ІдЉ†иЊУпЉМиАМз°ђйХАиЖЬжї§еЕЙзЙЗпЉИHard Coated Optical FiltersпЉЙеАЊеРСдЇОеЬ®еЕЙи∞±еЄ¶еЃљдЄКеЕЈжЬЙзЫЄељУеє≥еЭ¶зЪДдЉ†иЊУеИЖеЄГгАВ
еЄ¶еЃљ
еЄ¶еЃљжШѓдЄАдЄ™ж≥ҐйХњиМГеЫіпЉМзФ®дЇОи°®з§ЇдљњеЕ•е∞ДиГљйЗПйАЪињЗжї§еЕЙзЙЗзЪДеЕЙи∞±зЪДзЙєеЃЪйГ®еИЖгАВеЄ¶еЃљдєЯзІ∞дЄЇеНКйЂШеЕ®еЃљ пЉИFull Width Half MaximumпЉМFWHMпЉЙпЉМе¶ВеЫЊ54жЙАз§ЇпЉЪ

еЫЊ54 дЄ≠ењГж≥ҐйХњеТМеНКе≥∞еЕ®еЃљз§ЇжДПеЫЊ
FWHMжППињ∞дЇЖеЄ¶йАЪжї§ж≥ҐеЩ®дЉ†иЊУзЪДеЕЙи∞±еЄ¶еЃљгАВиѓ•еЄ¶еЃљзЪДдЄКйЩРеТМдЄЛйЩРеЃЪдєЙеЬ®жї§еЕЙзЙЗиЊЊеИ∞жЬАе§ІйАПе∞ДзОЗдЄАеНК зЪДж≥ҐйХње§ДгАВдЊЛе¶ВпЉМе¶ВжЮЬжї§еЕЙзЙЗзЪДжЬАе§ІйАПе∞ДзОЗдЄЇ 90%пЉМеИЩжї§еЕЙзЙЗиЊЊеИ∞ 45% йАПе∞ДзОЗзЪДж≥ҐйХње∞ЖеЃЪдєЙ FWHM зЪДдЄКйЩРеТМдЄЛйЩРгАВ10nm жИЦжЫіе∞ПзЪД FWHM 襀聧䪯жШѓз™ДеЄ¶пЉМйАЪеЄЄзФ®дЇОжњАеЕЙжЄЕзРЖеТМеМЦе≠¶ж£АжµЛгАВ25 вАУ 50nm зЪД FWHM йАЪеЄЄзФ®дЇОжЬЇеЩ®иІЖиІЙеЇФзФ®пЉЫиґЕињЗ 50nm зЪД FHWM 襀聧䪯жШѓеЃљеЄ¶пЉМйАЪеЄЄзФ®дЇОиНІеЕЙжШЊеЊЃйХЬеЇФзФ®гАВ
е±ПиФљиМГеЫіпЉИBlocking RangeпЉЙ
е±ПиФљиМГеЫіжШѓдЄАдЄ™ж≥ҐйХњйЧійЪФпЉМзФ®дЇО谮积襀濧еЕЙзЙЗи°∞еЗПзЪДиГљйЗПеЕЙи∞±еМЇеЯЯпЉИеЫЊ 55пЉЙгАВеЕґйШїжМ°з®ЛеЇ¶йАЪеЄЄдї•еЕЙеѓЖеЇ¶пЉИOptical DensityпЉЙжЭ•жМЗеЃЪгАВ

еЫЊ55 е±ПиФљиМГеЫіз§ЇжДПеЫЊ
еЕЙеѓЖеЇ¶пЉИOptical DensityпЉЙ
еЕЙеѓЖеЇ¶ (Optical DensityпЉМOD) жППињ∞дЇЖ襀濧еЕЙзЙЗйШїжМ°жИЦжЛТзїЭзЪДиГљйЗПгАВеЉПпЉИ28пЉЙдЄЇODжХ∞еАЉзЪДеЃЪдєЙпЉЪ
Percent\ Transmission=T=10^{-OD}\times100\%\\ OD=-log(\frac{T}{100\%})\\\tag{28}
йЂШODеАЉи°®з§ЇдљОйАПе∞ДзОЗпЉМдљОODеАЉи°®з§ЇйЂШйАПе∞ДзОЗгАВDOD=6 жИЦжЫіе§ІзЪДеЕЙеѓЖеЇ¶зФ®дЇОиЊГдЄЇжЮБзЂѓзЪДйШїжМ°йЬАж±ВпЉМдЊЛе¶ВжЛЙжЫЉеЕЙи∞±жИЦиНІеЕЙжШЊеЊЃйХЬгАВ3.0 вАУ 4.0 зЪДODеАЉжШѓжњАеЕЙеИЖз¶їеТМжЄЕзРЖгАБжЬЇеЩ®иІЖиІЙеТМеМЦе≠¶ж£АжµЛзЪДзРЖжГ≥йАЙжЛ©пЉМиАМOD= 2 жИЦжЫідљОеИЩжШѓйҐЬиЙ≤еИЖз±їеТМеИЖз¶їеЕЙи∞±й°ЇеЇПзЪДзРЖжГ≥йАЙжЛ©гАВ

еЫЊ56 еЕЙеѓЖеЇ¶еАЉпЉИODпЉЙдЄОйАПеЕЙзОЗзЪДеЕ≥з≥їеЫЊ
дЇМеРСиЙ≤жї§еЕЙзЙЗ
дЇМеРСиЙ≤жї§еЕЙзЙЗзФ®дЇОйАПе∞ДжИЦеПНе∞ДеЕЙзЪДжї§еЕЙзЙЗпЉМеЕЈдљУеПЦеЖ≥дЇОж≥ҐйХњпЉЫзЙєеЃЪж≥ҐйХњиМГеЫізЪДеЕЙ襀йАПе∞ДпЉМиАМдЄНеРМиМГеЫізЪДеЕЙ襀еПНе∞ДжИЦеРЄжФґе¶ВеЫЊ 57жЙАз§ЇпЉМеЬ®зЫЄеРМеПНе∞ДиІТдЄЛпЉМдЄНеРМзЪДж≥ҐйХњеЕЈжЬЙдЄНеРМзЪДеПНе∞ДдЄОйАПе∞ДжѓФдЊЛгАВдЇМеРСиЙ≤жї§еЕЙзЙЗйАЪеЄЄзФ®дЇОйХњйАЪпЉИlongpassпЉЙеТМзЯ≠йАЪпЉИshortpassпЉЙеЇФзФ®гАВ

еЫЊ57 дЇМеРСиЙ≤жї§еЕЙзЙЗжґВе±ВеПНе∞ДдЄОйАПе∞ДжѓФдЊЛз§ЇжДПеЫЊ
иµЈеІЛж≥ҐйХњпЉИCut-On WavelengthпЉЙ
иµЈеІЛж≥ҐйХњзФ®дЇОи°®з§ЇеЬ®йХњйАЪжї§ж≥ҐеЩ®дЄ≠йАПе∞ДзОЗеҐЮеК†еИ∞ 50% з©њйАПйЗПзЪДж≥ҐйХњгАВжИ™ж≠Ґж≥ҐйХњзФ±еЫЊ 58 дЄ≠зЪД ќї_{cut-on} и°®з§ЇгАВ

еЫЊ58 иµЈеІЛж≥ҐйХњ
жИ™ж≠Ґж≥ҐйХњпЉИCut-Off WavelengthпЉЙ
жИ™ж≠Ґж≥ҐйХњзФ®дЇОи°®з§ЇеЬ®зЯ≠йАЪжї§ж≥ҐеЩ®дЄ≠йАПе∞ДзОЗйЩНдљОеИ∞ 50% з©њйАПйЗПзЪДж≥ҐйХњгАВжИ™ж≠Ґж≥ҐйХњзФ±еЫЊ59дЄ≠зЪД ќї_{cut-off} и°®з§ЇгАВ

еЫЊ59 жИ™ж≠Ґж≥ҐйХњ
2.жї§еЕЙзЙЗеИґйА†жКАжЬѓ
дЄАиИђжЭ•иѓіпЉМжї§еЕЙзЙЗи¶БдєИйАЪињЗжЈїеК†жЬЙиЙ≤зОїзТГжИЦжЯУжЦЩжЭ•еРЄжФґдЄНйЬАи¶БзЪДеЕЙпЉМи¶БдєИйАЪињЗжЈїеК†еє≤жґЙжґВе±ВжЭ•еПНе∞ДдЄНйЬАи¶БзЪДеЕЙгАВе§Іе§ЪжХ∞жї§еЕЙзЙЗдї•еє≤жґЙжґВе±ВдЄЇеОЯеИЩпЉМйАЪињЗдЄУйЧ®йАЙжЛ©зЪДжґВе±ВиЃЊиЃ°еТМжЭРжЦЩжЭ•еЃЮзО∞жЙАйЬАзЪДйАПе∞ДжАІиГљгАВз°ђжґВе±Вжї§еЕЙзЙЗпЉИHard Coated Optical FiltersпЉЙйЗЗзФ®еНХдЄАеЯЇжЭРпЉМеЕЈжЬЙиЗіеѓЖжґВе±ВеТМеЗЇиЙ≤зЪДеЕЙе≠¶жАІиГљгАВеЃГдїђйЬАи¶Бжї°иґ≥ MIL-C-48497A дЄ≠иІДеЃЪзЪДйЩДзЭАеКЫгАБз£®жНЯгАБжЄ©еЇ¶еТМжєњеЇ¶и¶Бж±ВпЉМеЕЈжЬЙиЊГйЂШзЪДз≤ЊеЇ¶и¶Бж±ВгАВдЉ†зїЯйХАиЖЬжї§еЕЙзЙЗпЉИTraditional Coated Optical FiltersпЉЙйАЪеЄЄжШѓдЄАе†ЖеРЄжФґжЭРжЦЩгАБеє≤жґЙжґВе±ВеТМйЗСе±Юе±ВпЉМе±ВеОЛеЬ®дЄА赣嚥жИРдЄАдЄ™дљОжИРжЬђгАБйЂШжХИзЪДињЗжї§еЩ®пЉМзїДдїґзЪДе§НжЭВжАІйЩРеИґдЇЖињЩзІНжї§еЕЙзЙЗзЪДеЕЙе≠¶жАІиГљеТМзОѓеҐГз®≥еЃЪжАІгАВе∞љзЃ°е¶Вж≠§пЉМдЉ†зїЯзЪДжґВе±ВињЗжї§еЩ®ињШжШѓеЃЮй™МеЃ§иЃЊе§ЗеТМеИЖжЮРдї™еЩ®зЪДзРЖжГ≥йАЙжЛ©гАВжЬЙиЙ≤зОїзТГжї§еЕЙзЙЗпЉИColored Glass FiltersпЉЙеТМеЕґдїЦеРЄжФґжї§еЕЙзЙЗпЉИе¶Ве°СжЦЩжї§еЕЙзЙЗеТМ Wratten жї§еЕЙзЙЗпЉЙе∞ЖеЕГзі†гАБеМЦеРИзЙ©гАБжЯУжЦЩжИЦеЕґдїЦзЭАиЙ≤еЙВеЉХеЕ•еЯЇеЇХеЯЇжЭњпЉМдї•жОІеИґжї§еЕЙзЙЗзЪДеЕЙи∞±зЙєжАІгАВж≠§й°Южї§еЕЙзЙЗзЫЄеѓєдЊњеЃЬпЉМдљЖдЄОз±їдЉЉзЪДжґВе±Вжї§еЕЙзЙЗзЫЄжѓФпЉМеЕґеЕЙе≠¶жАІиГљдЄН姙зРЖжГ≥гАВеРЄжФґжї§еЕЙзЙЗйАЪеЄЄйЫЖжИРеИ∞зЕІжШОеТМдЉ†жДЯеЇФзФ®дЄ≠гАВ
дЉ†зїЯйХАиЖЬжї§еЕЙзЙЗеТМз°ђжґВе±Вжї§еЕЙзЙЗзЪДеМЇеИЂеЬ®дЇОеЯЇжЭРе±ВжХ∞гАВеЬ®дЉ†зїЯзЪДжґВе±ВеЄ¶йАЪжї§еЕЙзЙЗдЄ≠пЉМдЄНеРМжКШе∞ДзОЗзЪДжЭРжЦЩе±Вж≤ЙзІѓеЬ®е§ЪдЄ™еЯЇжЭњдЄКпЉМзДґеРОе∞ЖињЩдЇЫеЯЇжЭње§єеЬ®дЄАиµЈгАВдЊЛе¶ВпЉМжГ≥и±°еЫЊ60еЈ¶дЄ≠зЪДжґВе±ВйЗНе§НдЇЖе§ЪиЊЊ 100 жђ°пЉМзФЪиЗ≥иґЕињЗ 100 жђ°гАВињЩзІНжКАжЬѓдЉЪеѓЉиЗіжї§еЕЙзЙЗеПШеОЪиАМйАПе∞ДзОЗйЩНдљОгАВињЩзІНйАПе∞ДзОЗзЪДйЩНдљОжШѓзФ±дЇОеЕ•е∞ДеЕЙз©њињЗиЃЄе§Ъи°ђеЇХе±В庴襀聪е§Ъи°ђеЇХе±ВеРЄжФґеТМ/жИЦеПНе∞ДйА†жИРзЪДгАВзДґиАМеЬ®з°ђжґВе±ВеЄ¶йАЪжї§ж≥ҐеЩ®дЄ≠пЉМдЄНеРМжКШе∞ДзОЗзЪДжЭРжЦЩдїЕж≤ЙзІѓеЬ®еНХдЄ™еЯЇжЭњдЄКпЉИеЫЊ 60пЉЙгАВињЩзІНжКАжЬѓдЇІзФЯеЕЈжЬЙйЂШйАПе∞ДзОЗзЪДиЦДжї§еЕЙзЙЗгАВ

еЫЊ60 дЉ†зїЯжї§еЕЙзЙЗпЉИеЈ¶пЉЙеТМз°ђжЇЕе∞Джї§еЕЙзЙЗпЉИеП≥пЉЙ
3.жї§еЕЙзЙЗзЪДйЩРеИґ
зФ±дЇОжї§еЕЙзЙЗеРЄжФґйГ®еИЖж≥ҐйХњзФµз£БиЊРе∞ДпЉМињЩдЇЫ襀еРЄжФґзЪДзФµз£БиЊРе∞ДиГљйЗП襀蚐еМЦдЄЇзГ≠иГљпЉМеЫ†ж≠§ж≠§з±їжї§еЕЙзЙЗдЄНйАВзФ®дЇОйЂШеКЯзОЗзЪДеЕЙиЊРе∞ДгАВе§Іе§ЪжХ∞еОВеХЖзЪДдЇІеУБеЮЛељХйГљдЄНдЉЪж†ЗжШОиѓ•жї§ж≥ҐзЙЗжЙАиГљжЙњеПЧзЪДжЬАе§ІеЕЙеКЯзОЗпЉМдљЖжШѓйАЪеЄЄжГЕеЖµдЄЛйЭЮеРМи∞ГеЕЙжЇРзЪДжЩЃйАЪжї§ж≥ҐеЩ®дЄНиГљзФ®еЬ®еРМи∞ГеЕЙжЇРпЉМеН≥жњАеЕЙеЕЙжЇРдЄКпЉМдљЬиАЕжЫЊеЬ®еЃЮй™МеЃ§иІБиѓБињЗеЕґдїЦдЇЇеЃЮй™МдЄ≠е°СжЦЩжї§ж≥ҐзЙЗеЬ®жњАеЕЙдЄЛеЖТеЗЇиҐЕиҐЕзВКзГЯгАВеН≥дЊњжШѓзЇ≥з±≥зЇІдљНзІїжОІеИґеє≥еП∞дљњзФ®зЪДжњАеЕЙдЄУзФ®жї§ж≥ҐзЙЗпЉМдєЯжЬЙињЗ襀зГІеЭПзЪДзКґеЖµеПСзФЯгАВ
дЄГгАБеЕЙжЇРзЪД嚥еЉПдЄОйАЙжЛ©
еЬ®еЕЙе≠¶з≥їзїЯдЄ≠ж†єжНЃеЊЕжµЛзЙ©зЪДзЙєзВєдї•еПКжИРеГПзЪДйЬАж±ВпЉМжЬЙеЊИе§ЪдЄНеРМ嚥еЉПзЪДзЕІжШОжЦєж≥ХгАВеѓєдЇОжШЊеЊЃйХЬиАМи®АпЉМзЕІжШОз≥їзїЯйАЪеЄЄдЉЪиАГиЩСзІСеЛТзЕІжШОгАБдЄізХМзЕІжШОгАБжЪЧеЬЇзЕІжШОз≠ЙжШЊеЊЃйХЬзЙєжЬЙзЪДзЕІжШОжЦєеЉПгАВзІСеЛТзЕІжШОиѓЈиІБжЬђдЇЇдї•еЙНжЦЗзЂ†пЉЪ
иЗ≥дЇОдЄізХМзЕІжШОгАБжЪЧеЬЇзЕІжШОз≠ЙжШЊеЊЃйХЬзЕІжШОиЃЊиЃ°пЉМдї•еРОжЬЙжЬЇдЉЪеЖНеЖЩжЦЗзЂ†ињЫи°МељТзЇ≥жАїзїУгАВињЩйЗМеЕИйТИеѓєAOIеЄЄиІБзЪДзЕІжШО嚥еЉПињЫи°МзЃАеНХзЪДеИЖз±їпЉЪ
a.еЙНзЕІеЉПFront Illumination
еЙНзЕІеЉПзЕІжШОеЕЙжЇРеЭЗдљНдЇОзЫЄжЬЇдЄАдЊІпЉМдЊЭжНЃеЕЙзЇњжМЗеРСзЪДзЙєеЊБеПѓеИЖдЄЇдї•дЄЛеЗ†з±їпЉЪ
1.зЫіеРСеЮЛеЙНеЕЙжЇРDirectional Front Lighting
зЫіеРСеЮЛеЙНеЕЙжЇРдЄ≠еЕЙжЇРдЄНеБЪдїїдљХиБЪеЕЙгАБжХ£е∞Де§ДзРЖпЉМдїЕеЬ®зЫЄжЬЇдЄАдЊІеѓєеЊЕжµЛзЙ©ињЫи°МзЕІжШОпЉМзЕІжШОиІТеЇ¶йАЪеЄЄдЄОзЫЄжЬЇдЄНеРМиљігАВеЊЕжµЛзЙ©и°®йЭҐиµЈдЉПињЗе§ІеПѓиГљдЉЪеЗЇзО∞йШіељ±пЉМиЛ•еѓєдЄНеЄМжЬЫеЊЕжµЛзЙ©дЄКе≠ШеЬ®йШіељ±ж≠§з±їзЕІжШОе∞±дЄНйАВзФ®гАВ

еЫЊ61 зЫіеРСеЮЛеЙНеЕЙжЇР
2.жЙ©жХ£еЮЛеЙНеЕЙжЇРDiffuse Front Lighting
жЙ©жХ£еЮЛеЙНеЕЙжЇРеЬ®зЫіеРСеЮЛеЙНеЕЙжЇРеЯЇз°АдЄКдЇОеЕЙжЇРеЙНжФЊеҐЮеК†жХ£е∞ДзЙЗпЉИDiffused PlateпЉЙе∞ЖеЕЙжЇРдї•жХ£е∞ДзЪД嚥еЉПжКХеРСеЊЕжµЛзЙ©гАВињЩж†ЈжКХе∞ДзЪДеЕЙжЇРиЊГдЄЇжЯФеТМпЉМеН≥дЊњдЇІзФЯеЊЕжµЛзЙ©и°®йЭҐйШіељ±еЕґйШіељ±зЪДжШОжЪЧињЗеЇ¶дєЯдЄНдЉЪеГПзЫіеРСеЮЛеЙНеЕЙжЇРйВ£ж†ЈеЉЇзГИгАВ

еЫЊ62 жЙ©жХ£еЮЛеЙНеЕЙжЇР
3.з΃嚥еЙНеЕЙжЇРRing Front Lighting
з΃嚥еЙНеЕЙжЇРйАЪеЄЄзОѓзїХзЭАзЫЄжЬЇжИЦиАЕзЙ©йХЬеѓєеЊЕжµЛзЙ©ињЫи°МзЕІжШОпЉМеЕґеЕЙжЇР嚥зКґдЄЇзОѓи£ЕпЉМеПѓдї•жШѓз΃嚥зЪДзБѓзЃ°пЉМдєЯеПѓдї•жШѓз΃嚥зЪДLEDйШµеИЧгАВ

еЫЊ63 з΃嚥еЙНеЕЙжЇР
е¶ВеЫЊ64жЙАз§ЇдЄЇkeyenceжШЊеЊЃйХЬзЪД10XзЙ©йХЬпЉМињЩдЄ™зЙ©йХЬе∞±йЕНжЬЙз΃嚥еЙНеЕЙжЇРдљЬдЄЇиЊЕеК©зЕІжШОпЉМеПѓзФ®дЇОдљОеПНе∞ДзОЗи°®йЭҐињЫи°МеИЭж≠•еѓєзД¶з≠ЙеЇФзФ®еЬЇжЩѓжПРйЂШеЊЕжµЛзЙ©и°®йЭҐдЇЃеЇ¶гАВ

еЫЊ64 keyenceжШЊеЊЃйХЬ10XзЙ©йХЬзЪДз΃嚥еЙНеЕЙжЇР
4.дљОиІТеЇ¶еЙНеЕЙжЇРOblique Front Lighting
еЕЙжЇРдїОдЊІеРСеѓєеЊЕжµЛзЙ©и°®йЭҐињЫи°МзЕІжШОгАВж≠§ељҐеЉПзЪДеЕЙжЇРйАВзФ®дЇОйЂШеПНе∞ДзОЗзЪДеЊЕжµЛзЙ©и°®йЭҐпЉМйБњеЕНе§ІйЗПеЕ®еПНе∞ДеѓєзЫЄжЬЇзЪДељ±еУНгАВ

еЫЊ65 дљОиІТеЇ¶еЙНеЕЙ
5.еРМиљіеЙНеЕЙжЇРCoaxial Front Lighting
ињИеЕЛзФЯпЉИMichaelsonпЉЙеЉПжЮґжЮДзЪДжШЊеЊЃйХЬйАЪеЄЄдЉЪдљњзФ®ж≠§зІНеЕЙжЇРзЕІжШОпЉМйЕНеРИдї•зІСеЛТзЕІжШОзЪДйХЬзїДжЮґеН≥еПѓеЬ®еЊЕжµЛзЙ©дЄКиОЈеЊЧзЂЦзЫіжЦєеРСдЄКзЪДеЭЗеМАзЕІжШОгАВж≠§ељҐеЉПзЪДеЕЙжЇРйАЪеЄЄдЄНдїЕеЕЈе§ЗжИРеГПзЕІжШОзЪДеКЯиГљпЉМеЬ®ж≠§з±їеЮЛзЪДеє≤жґЙдї™дЄ≠ињШдЉЪдљЬдЄЇеЕЙз®ЛеЈЃеЕЈжЬЙеЊЕжµЛи°®йЭҐйЂШеЇ¶дњ°жБѓзЪДеє≤жґЙеЕЙгАВ

еЫЊ66 еРМиљіеЙНеЕЙ
е¶ВеЫЊ67жЙАз§ЇдЄЇkeyenceжШЊеЊЃйХЬпЉМеЕґеЖЕйГ®зЪДеРМиљіеЕЙжЇРйЕНеРИеЕґзЩљеЕЙеє≤жґЙж®°зїДеН≥еПѓињЫи°МзЩљеЕЙеє≤жґЙжЙЂжППжЬѓзЪДйЗПжµЛгАВ

еЫЊ67 keyenceеЊЃйХЬ10XзЙ©йХЬзЪДеРМиљіеЕЙжЇР
b.иГМзЕІеЉПBack Illumination
1.зЫіеРСеЮЛиГМеЕЙжЇРDirection Back Lighting
зЫіеРСеЮЛиГМеЕЙжЇРеЕЄеЮЛзЪДеЇФзФ®еЬЇжЩѓе∞±жШѓжКХељ±дї™пЉМеЕЙжЇРдєЛдЄКзЪДж†ЈеУБпЉИsampleпЉЙйАЪеЄЄжШѓеПѓйАПеЕЙзЪДгАВ

еЫЊ68 зЫіеРСеЮЛиГМеЕЙжЇР
2.жЙ©жХ£еЮЛиГМеЕЙжЇРDiffuse Back Lighting
жЙ©жХ£еЮЛиГМеЕЙжЇРйАЪеЄЄзФ®дЇОеєњеСКзЙМпЉМзЫЄиЊГдЇОзЫіеРСеЮЛиГМеЕЙжЇРеЕґи°®йЭҐеҐЮеК†дЇЖжХ£е∞ДзЙЗгАВзФ±дЇОиѓ•зІНеЕЙжЇРеЬ®еЊИе§ІиІТеЇ¶иМГеЫіеЖЕеЭЗеПѓзЬЛеИ∞иґ≥е§ЯдЇЃеЇ¶зЪДгАБеЭЗеМАжХ£е∞ДзЪДеЕЙпЉМеЫ†ж≠§еєњеСКзЙМдљњзФ®ж≠§з±їеЕЙжЇРпЉМеПѓдљњеЬ®жЫіе§ЪдЄНеРМдљНзљЃдЄКзЪДдЇЇдї•жЯФеТМзЪДеЕЙзЇњжДЯиІЙзЬЛеИ∞еєњеСКзЙМдЄКзЪДеЖЕеЃєгАВ

еЫЊ69 жЙ©жХ£еЮЛиГМеЕЙжЇР
c.е§НеРИеЕЙжЇРHybrid light source
е§НеРИеЕЙжЇРзїУеРИеРДзІНеРДж†ЈзЪДзЕІжШО嚥еЉПпЉМе¶ВеЙНйЭҐзЪДkeyenceжШЊеЊЃйХЬ10XзЙ©йХЬпЉМе∞±жШѓе¶ВеЫЊ70жЙАз§ЇзЪДе§НеРИеЕЙжЇРпЉМйЫЖеРИдЇЖеРМиљіеЙНеЕЙжЇРдЄОз΃嚥еЙНеЕЙжЇРпЉМзФ®дї•еЇФеѓєе§ЪзІНе§Ъж†ЈзЪДеЊЕжµЛзЙ©жПРдЊЫжЬАдљ≥жИРеГПзЪДзЕІжШОгАВ

еЫЊ70 е§НеРИеЕЙжЇРз§ЇжДПеЫЊ
еЕЂгАБеЕЙе≠¶иљѓдїґдЄ≠зЪДеЕЙжЇРж®°жЛЯ
жЬђдЇЇдЄїи¶БдљњзФ®CODEVгАБLighttoolsгАБZEMAXдЄЙзІНеЕЙе≠¶ж®°жЛЯиљѓдїґпЉМеЕґдЄ≠CODEVдЄїи¶БзФ®дЇОйХЬе§іиЃЊиЃ°пЉМдЄОZEMAXзЪДеЇПеИЧж®°еЉПпЉИSequential ModeпЉЙз±їдЉЉпЉМеѓєдЇОеЕЙжЇРзЪДеЃЪдєЙдїЕдЄЇеНХзЇѓзЪДеРДзІНж≥ҐйХњгАБиІЖеЬЇпЉИFieldпЉЙеЃЪдєЙпЉМеЬ®ж≠§еЯЇз°АдєЛдЄКеѓєеГПеЈЃз≠ЙеПШйЗПињЫи°МдЉШеМЦпЉМдЄНиАГиЩСеЕЙе≠¶з≥їзїЯдЄ≠зЪДжЭВжХ£еЕЙгАВйАЪеЄЄжИСдїђдЉЪе∞ЖCODEVиЃЊиЃ°е•љзЪДйХЬзїДеѓЉеЕ•LighttoolsдЄ≠ињЫи°МзЕІжШОж®°жЛЯпЉМињЩдЄАж≠•з±їдЉЉдЇОZEMAXзЪДйЭЮеЇПеИЧж®°еЉПпЉИNon-Sequential ModeпЉЙпЉМйТИ僺襀еЃЪдєЙеЗ†дљХ嚥зКґзЪДеЕЙжЇРдї•еПКзЫЄеЇФзЪДеЕЙзЇње±ЮжАІињЫи°МйАРдЄ™еЕЙзЇњзЪДеЕЙзЇњињљиЄ™пЉМжЬАзїИжИСдїђеПѓдї•иОЈеЊЧеМЕжЛђжЭВжХ£еЕЙеЬ®еЖЕзЪДеЕЙе≠¶з≥їзїЯеЖЕжЬАдЄЇжЛЯзЬЯзЪДзЕІжШОж®°жЛЯзїУжЮЬгАВињЩйЗМдЄїи¶БдїЛзїНLighttoolsдЄОZEMAXеЬ®еЕЙжЇРж®°жЛЯдЄ≠еѓєеЕЙжЇРеЃЪдєЙзЪДдЄїи¶БеПВжХ∞дЄОзЙєеЊБгАВ
1.Lighttools
LighttoolsжЧҐеПѓдї•иЗ™еЈ±зїШеИґеРДзІНеРДж†ЈзЪДеЗ†дљХдљУдЄЇеЕґжЭРиі®гАБи°®йЭҐеЃЪдєЙзЫЄеЇФзЪДеЕЙе≠¶жАІиі®пЉМдєЯеПѓдї•еѓЉеЕ•SolidWorksзїШеИґе•љзЪДе§НжЭВзїУжЮДдї•еПКCODEVиЃЊиЃ°е•љзЪДе§НжЭВйХЬзїДпЉМжЮДжИРжЫідЄЇе§НжЭВзЪДеЕЙе≠¶з≥їзїЯињЫи°МзЕІжШОж®°жЛЯгАВдЊЛе¶ВпЉМ670жµБжШОзЪДзїњеЕЙзВєеЕЙжЇРпЉМжФЊеЬ®еє≥йЭҐжЬ®жЭњпЉИ100* 100 * 10 mm ^ 3пЉЙеЙНйЭҐпЉМзЫЄиЈЭ200mmпЉМжШЊз§ЇжЬ®жЭњдЄ≠зЪДзЕІжШОеИЖеЄГпЉМжИСдїђеПѓдї•зЫіжО•еЬ®lighttoolsдЄ≠жФЊзљЃдЄАдЄ™зВєеЕЙжЇРеєґеЃЪдєЙеЃГзЪДеЕЙеКЯзОЗгАБж≥ҐйХњз≠ЙжАІиі®пЉЪ

еЫЊ71 еЃЪдєЙзВєеЕЙжЇРзЪДеЕЙеКЯзОЗз≠ЙжАІиі®

еЫЊ72 еЃЪдєЙзВєеЕЙжЇРзЪДеЕЙи∞±з≠ЙжАІиі®
еЬ®иЃЊеЃЪеЕЙзЇњињљињєзЪДеЕЙзЇњжХ∞йЗПдєЛеРОпЉМеН≥еПѓеЬ®иЃЊеЃЪе•љзЪДж®°еЮЛдЄКж®°жЛЯеЕЙзЕІеИЖеЄГпЉЪ

еЫЊ73 иЃЊеЃЪеЕЙзЇњињљињєзЪДеЕЙзЇњжХ∞йЗП

еЫЊ74 ж®°жЛЯеЕЙзЕІеИЖеЄГ

еЫЊ75 ж®°жЛЯеЕЙзЕІеИЖеЄГзЕІеЇ¶еИЖеЄГзїУжЮЬ
еЖНдЊЛе¶ВпЉМе∞ЖдЄЙйАПйХЬйХЬзїДпЉИ Triplet lensпЉЙдїОCODEVеѓЉеЕ•LighttoolsпЉМйХЬзїДEFL=100mmпЉМf/#=5пЉМзЙ©дљУиЈЭз¶їдЄЇ300mmпЉМеИЩдїОLighttoolsдЄ≠еПѓзїШеИґжХідЄ™зЕІжШОж®°жЛЯзЪД3DеЫЊгАВй¶ЦеЕИж†єжНЃи¶БеОїеЬ®CODEVдЄ≠иЃЊеЃЪдЄЙйАПйХЬйХЬзїДзЪДеПВжХ∞пЉМеЊЧеИ∞зЫЄеЇФзЪДдЄЙйАПйХЬйХЬзїДж®°еЮЛпЉЪ

еЫЊ76 CODEVдЄ≠иЃЊеЃЪдЄЙйАПйХЬйХЬзїДзЪДеПВжХ∞

еЫЊ77 CODEVдЄ≠дЄЙйАПйХЬйХЬзїД3Dж®°еЮЛ
зДґеРОе∞ЖеЕґеѓЉеЕ•LighttoolsпЉМиЃЊеЃЪеЕЙжЇРдњ°жБѓеРОињЫи°МеЕЙзЇњињљињєпЉМеН≥еПѓеЊЧеИ∞иѓ•йХЬзїДзЪДзЕІжШОж®°жЛЯгАВ

еЫЊ78 еѓЉеЕ•LighttoolsеРОињЫи°МеЕЙзЇњињљињє

еЫЊ79 йХЬзїДзЪДзЕІжШОж®°жЛЯињСжЩѓеЫЊ
дї•дЄКдЄ§дЄ™ж°ИдЊЛжЭ•иЗ™жИСзЪДиѓЊз®ЛдљЬдЄЪгАВжЫіе§ЪLighttoolsзЕІжШОж®°жЛЯиѓіжШОпЉМеПѓиѓ¶иІБLighttoolsжУНдљЬжЙЛеЖМпЉЪIllumination Module UserвАЩs Guide еИЖеЖМпЉМLighttoolsеЃЙи£ЕжЦЗдїґе§єдЄЛжРЬ糥PDFеН≥еПѓжЙЊеИ∞зЫЄеЕ≥жУНдљЬжЙЛеЖМзЪДPDFжЦЗдїґгАВ
2.ZEMAX
ZEMAXињЫи°МеЕЙжЇРж®°жЛЯйАЪеЄЄеЬ®йЭЮеЇПеИЧж®°еЉПпЉИNon-Sequential ModeпЉЙдЄЛињЫи°МгАВињЩдЄАйГ®еИЖеЖЕеЃєеПѓеПВиАГZEMAXеПСеЄГзЪДGetting Started With OpticStudio жЙЛеЖМпЉМжХЩе≠¶йГ®еИЖзЪДжХЩе≠¶6пЉЪйЭЮеЇПеИЧеЕЙзЇњињљињєз≤Њи¶БдїЛзїНе¶ВдљХж®°жЛЯеЕЙжЇРгАВйАЪеЄЄеЬ®ZEMAXеЃЙи£ЕжЦЗдїґе§єдЄЛжРЬ糥PDFеН≥еПѓжЙЊеИ∞зЫЄеЕ≥PDFжЦЗдїґпЉМдєЯеПѓдї•иЗ™еЈ±жЙЊиµДжЇРпЉЪ
йЭЮеЇПеИЧж®°еЉПеПѓзФ®дЇОж®°жЛЯзЕІжШОз≥їзїЯпЉМе∞§еЕґжШѓеЕЈжЬЙе§ЪдЄ™жИЦе§НжЭВеЕЙжЇРзЪДзЕІжШОз≥їзїЯгАВйЭЮеЇПеИЧж®°еЉПдЄЛеЕЙзЇњињљињєжЧґдЄНеБЗеЃЪдїїдљХйҐДеЃЪиЈѓеЊДпЉМеЕЙзЇњдЇОиЃЊеЃЪзЪДеЕЙжЇРдЄКе∞ДеЗЇеРОдЉЪдЊЭзЕІжКШе∞ДгАБеПНе∞ДеЃЪеЊЛпЉМдї•еПКйҐДиЃЊе•љзЪДйХЬзїДгАБи°®йЭҐзЪДжКШе∞ДзОЗгАБеПНе∞ДзОЗпЉМдЄОеЕЙз®ЛдЄКзЪДдЄАеИЗзЙ©дїґдЇ§дЇТдљЬзФ®пЉМеПѓиГљеПНе∞ДгАБжКШе∞ДгАБзїХе∞ДгАБжХ£е∞ДгАБеИЖи£ВдЄЇдЄ§жЭЯеЕЙзЇњз≠ЙгАВ
йЭЮеЇПеИЧж®°еЉПдЄЛпЉМеПѓеЬ®йЭЮеЇПеИЧж®°еЉПзЪДзЉЦиѓСеЩ®дЄЛзЪДObeject TypeдЄ≠иЃЊеЃЪеЕЙжЇРзЙ©дїґпЉЪ

еЫЊ80 йЭЮеЇПеИЧж®°еЉПзЪДзЉЦиѓСеЩ®

еЫЊ81 йЭЮеЇПеИЧж®°еЉПзЪДзЉЦиѓСеЩ®еПѓйАЙжЛ©зЪДеЕЙжЇР嚥еЉП
жЙУеЉАдЄАдЄ™иМГдЊЛжЦЗдїґпЉЪвАЬDigital Projector Flys Eye Homogenizer.zmxвАЭпЉМињЩжШѓдЄАдЄ™ж§≠зРГеЕЙжЇРзЙ©дїґгАБйЭЮзРГйЭҐи°®йЭҐеПНе∞ДйХЬгАБдЄ§дЄ™е§НзЬЉйАПйХЬйШµеИЧдЄОдЄАиИђйАПйХЬжЮДжИРзЪДеЕЙе≠¶з≥їзїЯпЉМзїЩдЄАдЄ™зїЩеЃЪи°®йЭҐжПРдЊЫжֺ嚥зЪДзЕІжШОеЬЇгАВ

еЫЊ82 Digital Projector Flys Eye Homogenizer.zmx
дЄКеЫЊдЄ≠зЪДжѓПдЄ™йЫґдїґеЬ®зЉЦиѓСеЩ®дЄ≠йГљдї•дЄАдЄ™зЙ©дїґжЭ•и°®з§ЇпЉМеИЖеИЂеЃЪдєЙеЕґеЕЙе≠¶жАІиі®пЉМеЬ®жЬАзїИзЪДеЕЙе±Пеє≥йЭҐдЄКиОЈеЊЧжКХе∞ДеЕЙеИЖеЄГпЉМињЩдЊњжШѓZEMAXзЪДеЕЙе≠¶зЕІжШОж®°жЛЯгАВ

еЫЊ83 Digital Projector Flys Eye Homogenizer.zmxзЉЦиѓСеЩ®
зїЖиКВеЖЕеЃєиѓ¶иІБGetting Started With OpticStudio жЙЛеЖМгАВ
еРОиЃ∞
зЃЧжШѓеЖЩеЗЇдЇЖдЄ™жЮґжЮДпЉМжЬЙз©ЇеЖНдЄ∞еѓМеРІгАВ
еЫЮе§ізЬЛдї•еЙНдЄКиѓЊзЪДиѓЊжЬђиЃ≤дєЙпЉМеЕґеЃЮйВ£дЇЫдљЬиАЕгАБжХЩжОИдєЯзЬБзХ•гАБеБЈеЈ•еЗПжЦЩдЇЖеЊИе§ЪеЖЕеЃєгАВзїЉеРИжАІгАБиЈ®йҐЖеЯЯз†Фз©ґе∞±жШѓињЩж†ЈеЖЧжЭВпЉМиГљжИРеКЯеїЇжЮДдЄАдЄ™зЯ•иѓЖдљУз≥їе∞±зЃЧжИРеКЯдЄАеНКгАВжАїжЬЙдЇЇиѓідЄАдЄ™дЇЇдЄНеПѓиГљеРДзІНзІСзЫЃж†Јж†ЈйГљз≤ЊйАЪпЉМељУзДґдЄНеПѓиГљпЉМдљЖиµЈз†БеЬ®еБЪзїЉеРИжАІзЪДдЄАдЄ™з≥їзїЯжЧґпЉМйБЗеИ∞йЪЊзВєиГље§ЯењЂйАЯеЗЖз°ЃжДПиѓЖеИ∞еЕґзЧЗзїУпЉМеєґиГље§ЯењЂйАЯе≠¶дє†зЫЄеЕ≥еЖЕеЃєпЉМиГље§ЯиІ£еЖ≥йЧЃйҐШжЙНжШѓжЬАзїИзЫЃзЪДгАВеРСжЭ•еЇФиѓ•ињљж±ВзЪДйГљдЄНжШѓж†Јж†Јз≤ЊйАЪпЉМиАМжШѓиГље§Яж†Јж†Јз≤ЊйАЪзЪДиГљеКЫпЉМдњЭжМБзїИзФЯе≠¶дє†зЪДиГљеКЫгАВ
еПВиАГ
- ^World&#x27;s oldest telescope? http://news.bbc.co.uk/2/hi/science/nature/380186.stm
- ^жЭ®еЖЫжШМ,жЃµиЙ≥дЄљ.&quot;дЄ≠еЫљжЧ©жЬЯйШ≥зЗІзЪДеЗ†дЄ™йЧЃйҐШ.&quot; дЄЬеНЧжЦЗеМЦ .08(2000):101-103.¬†https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2000&filename=DNWH200008016&uniplatform=NZKPT&v=WAmxsIsOejXOsPFzceMAvXyrGZra6-In94uE2d_NiFWJyIrjI0z_vDgUeVaoZq9t
- ^зГЬ¬†https://baike.baidu.com/item/%E7%83%9C/6905559?fr=aladdin
- ^ж±ЮеЕЙи∞±¬†https://zh.wikipedia.org/wiki/%E6%B1%9E#/media/File:Mercury_spectrum_experiment.jpg
- ^Schanda, J. ed., 2007. Colorimetry: understanding the CIE system. John Wiley & Sons. https://zh.book4you.org/book/737680/5655e6
- ^CIE 1931 XYZ Color Matching Functions https://zh.wikipedia.org/wiki/File:CIE_1931_XYZ_Color_Matching_Functions.svg
- ^Application Notes: Designing Backlight Displays in LightTools
- ^https://protonsforbreakfast.wordpress.com/2013/12/10/looking-on-the-bright-side/
- ^https://www.nml.org.tw/measurement/new-knowledge/3603-%E5%85%89%E5%BC%B7%E5%BA%A6%E7%9A%84%E5%96%AE%E4%BD%8D%EF%BC%9A%E7%87%AD%E5%85%89.html
- ^Spectral power distribution of a 25 W incandescent light bulb https://commons.wikimedia.org/wiki/File:Spectral_power_distribution_of_a_25_W_incandescent_light_bulb.png
- ^https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=884
- ^https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=2692
- ^https://sites.google.com/view/ntupmlab/йЗПжЄђжЬНеЛЩ?authuser=0
- ^https://revox.jp/en/products/SLG-150V_165V/
- ^https://zh.wikipedia.org/wiki/%E9%AB%98%E5%BC%B7%E5%BA%A6%E6%B0%A3%E9%AB%94%E6%94%BE%E9%9B%BB%E7%87%88
- ^https://www.researchgate.net/publication/252185356_Probing_Stark_atoms/figures?lo=1
|
|