麦克斯韦方程组以一种近乎完美的方式统一了电和磁,并预言光就是一种电磁波,这是物理学家在统一之路上的巨大进步。 这个方程组是用积分和微分的形式写的,并不简单直观,但是它的物理内涵确是非常简单的。
01电磁统一之路
电和磁并没有什么明显的联系,科学家一开始也是独立研究电现象和磁现象的。 1820年,奥斯特在一次讲座上偶然发现通电的导线让旁边的小磁针偏转了一下,他立马针对这个现象进行了三个月的穷追猛打,最后发现了电流的磁效应,也就是说电流也能像磁铁一样影响周围的小磁针。 三个月,毕奥和萨伐尔在大佬拉普拉斯的帮助下就找到了电流在空间中产生磁场大小的定量规律,这就是著名的毕奥-萨伐尔定律。用毕奥-萨伐尔定律,我们就可以算出任意电流在空间中产生磁场的大小,但是这种方法在实际使用的时候会比较繁琐。 又过了两个月之后,安培发现了一个更实用更简单的计算电流周围磁场的方式,这就是安培环路定理。安培还总结了一个很实用的规律来帮你判断电流产生磁场的方向,这就是安培定则(也就是高中学的右手螺旋定则)。 直到11年后的1831年,天才实验物理学家法拉第发现了磁生电的规律,也就是电磁感应定律。法拉第发现磁能生电的关键就是:他发现静止的磁并不能生电,一定要变化的磁才能生电。 然后,麦克斯韦就对安培环路定理进行了扩充,加入了变化的电场也能产生磁场。 麦克斯韦方程组描述了经典电磁学的一切,而且它是由四个方程组成的。 第一个方程描述电,第二个方程描述磁,第三个方程描述磁如何生电,第四个方程描述电如何生成磁。
02库仑的发现
两个电荷之间的静电力与两者的电荷量有关,而且还是电荷越大静电力越大,加上距离平方反比规律,两个电荷之间的静电力的公式如下: 这就是库伦定律:两个电荷之间的静电力跟两个电荷量的乘积成正比,跟它们距离的平方成反比,剩下的都是常数。q1、q2就是两个电荷的电荷量,ε0是真空的介电常数。
库伦定律是一个实验定律,也就说库伦做了很多实验发现两个电荷之间确实存在着一个这么大小的静电力,但是它并没有告诉你这个静电力是如何传递的。两个并没有接触的物体之间存在某种力,一个常见的想法就是这两个物体之间存在着某种我们看不见的东西在帮它们传递作用力,有人认为是以太,有人认为是某种弹性介质,但是法拉第说是力线,而且这种力线不是什么虚拟的辅助工具,而是客观的物理实在。它可以传递作用力,也可以具有能量。这些思想慢慢形成了我们现在熟知的场。电荷会在周围的空间中产生一个电场,这个电场又会对处在其中的电荷产生一个力的作用。这个电场的强度越大,电荷受到的力就越大,正电荷受力的方向就是这点电场的方向。所以,电场具有大小和方向,这是一个矢量。为了直观形象的描述电场,我们引入了电场线。电场线的密度刚好就代表了电场强度的大小,而某点电场线的切线方向就代表了该处电场的方向。一个正电荷就像太阳发光一样向四周发射电场线,负电荷就汇集电场线。
由库伦定律就可以根据这个求出一个点电荷周围的电场强度。如果有很多个电荷,就把每个电荷在这点产生的电场强度算出来,再把它们叠加起来就行了。如果这是一个连续的带电体(比如一根带电的线),就用微积分把这个带电体切成无数个无穷小的部分,这样每一个无穷小的部分就可以看做一个点电荷,然后把这无数个点电荷在那点产生的电场强度叠加起来(就是积分)就行了。我们知道,之所以会有电场线,是因为空间中存在电荷。而且,电荷的电量越大,它产生的电场强度就越大,电场线就越密,那么穿过塑料袋的电场线的数量就越多,对应的电通量就越大。通过一个闭合曲面的电通量跟曲面内包含电荷总量是成正比的,电荷量越大,通过这个任意闭合曲面的电通量就越大,反之亦然。这就是麦克斯韦方程组的第一个方程——高斯电场定律的核心思想。问题1:我们假设空间里有一个电场强度为E的匀强电场,然后有一个面积为a的木板跟这个电场方向垂直,那么,通过这个木板的电通量Φ要怎么表示呢?
电场线通过一个曲面的数量表示电通量。电场线的密度代表了电场强度的大小。所以,电场强度越大,通过木板的电场线数量越多;木板的面积越大,通过木板的电场线数量越多。而电场线的数量越多,就意味着电通量越大。因为电场强度E是一个矢量(有大小和方向),所以我们用E的绝对值|E|来表示E的大小,那么我们直接用电场强度的大小|E|和木板面积a的乘积来表示电通量的大小是非常合理的。也就是说,通过木板的电通量Φ=|E|×a。问题2:还是上面的木板和电场,如果木板跟电场的方向不是垂直的,它们之间有一个夹角θ,那这个电通量又要怎么求呢?
如上图,首先,我们能直观地感觉到:当木板不再和电场方向垂直的时候,这个木板被电场线穿过的有效面积减小了。现在真正能够有效挡住电场线的变成了BC这个面。我们是用一个垂直于这个平面的向量的方向表示这个平面的方向,这个向量就叫这个平面的法向量。如上图所示,我画了一个跟木板垂直的法向量n,那么这个法向量n和电场E的夹角才是木板这个平面和电场的夹角θ。AB、BC和θ之间存在一个非常简单的三角关系:BC=AB×cosθ,那此时通过木板的电通量就变成了:Φ=|E|×|a|×cosθ。标量因为只有大小没有方向,所以标量的乘法可以直接像代数的乘法一样,让它们的大小相乘就行了。矢量因为既有大小又有方向,所以你两个矢量相乘就不仅要考虑它的大小,还要考虑它的方向。点乘(符号为‘·’)就是让一个矢量的投影和另一个矢量的大小相乘,这样就既体现了大小又体现了方向。
如上图,我们有两个矢量OA和OB(线段的长短代表矢量的大小,箭头的方向代表矢量的方向),我们过A点做AC垂直于OB(也就是OA往OB方向上投影),那么线段OC的长度就代表了矢量OA在OB方向上的投影。而根据三角函数的定义,一个角度θ的余弦cosθ被定义为邻边(OC)和斜边(OA)的比值,即cosθ=OC/|OA|(绝对值表示矢量的大小,|OA|表示矢量OA的大小)。所以矢量OA在OB方向上的投影OC可以表示为:OC=|OA|×cosθ。 既然两个矢量的点乘被定义为一个矢量的投影和和另一个矢量大小的乘积,现在我们已经得到了投影OC的表达式,那么矢量OA和OB的点乘就可以表示为:OA·OB=OC×|OB|=|OA||OB|cosθ。电场强度也是一个矢量,它有大小也有方向(电场线的密度代表大小,电场线的方向代表它的方向);平面其实也是一个矢量,平面的大小不用说了,平面的方向是用垂直于这个平面的法向量来表示的。电场E通过一个平面a的电通量Φ就可以表示为这两个矢量(电场和平面)的点乘,即Φ=E·a(因为根据点乘的定义有E·a=|E|×|a|×cosθ)。我们可以把一个曲面分割成许多块,只要我们分割得足够细,保证每一小块都足够小,那么我们是可以把这个小块近似当作平面来处理的。而且不难想象,我把这个曲面分割得越细,它的每一个小块就越接近平面,我们把这些小平面都加起来就会越接近这个曲面本身。如果我们把这个曲面分割成无穷多份,这样每个小块的面积就都是无穷小,于是我们就可以认为这些小块加起来就等于这个曲面了。这就是微积分最朴素的思想。
如上图,我们把一个球面分割成了很多块,这样每一个小块就变成了一个长为dx,宽为dy的小方块,这个小方块的面积da=dx·dy。如果这个小块的电场强度为E,那么通过这个小块的电通量就是E·da。如果我们把这个球面分割成了无穷多份,那么把这无穷多个小块的电通量加起来,就能得到穿过这个曲面的总电通量。一个小块da的电通量是E·da,那么我们就可以用下面的符号表示通过这个曲面S的总电通量:
这个拉长的大S符号就是积分符号,它就是我们上面说的微积分思想的代表。它的右下角那个S代表曲面S,也就是说我们这里是把这个曲面S切割成无穷小块,然后对每一块都求它的通量E·da,然后把通量累积起来。至于这个大S中间的那个圆圈就代表这是一个闭合曲面。高斯电场定律的核心思想就是:通过闭合曲面的电通量跟这个曲面包含的电荷量成正比。那么,这就是麦克斯韦方程组的第一个方程——高斯电场定律了:
方程的左边,就是电场E通过闭合曲面S的电通量。方程右边带enc下标的Q表示闭合曲面内包含的电荷总量,ε0是个常数(真空介电常数)。等号两边一边是闭合曲面的电通量,另一边是闭合曲面包含的电荷。库伦定律从点电荷的角度描述静电,而高斯电场定律则从通量的角度来描述静电。磁通量的概念很好建立,可以完全模仿电通量的概念,将磁感线通过一个曲面的数量定义磁通量。因为磁场线的密度一样表征了磁感应强度的大小。所以磁感应强度为B的磁场通过一个平面a的磁通量Φ表示为Φ=B·a。
高斯磁场定律,它是核心思想似乎就应该是:通过闭合曲面的磁通量跟这个曲面包含的“磁荷量”成正比。然而这里会有个问题,我们知道自然界中有独立存在的正负电荷,电场线都是从正电荷出发,汇集与负电荷。但是自然界里并不存在(至少现在还没发现)独立的磁单极子,任何一个磁体都是南北两极共存。所以,磁感线跟电场线不一样,它不会存在一个单独的源头,也不会汇集到某个地方去,它只能是一条闭合的曲线。
上图是一个很常见的磁铁周围的磁感线,磁铁外部的磁感线从N极指向S极,在磁铁的内部又从S极指向N极,这样就形成一个完整的闭环。如果你在这个闭环里画一个闭合曲面,那么结果肯定就是有多少根磁感线从曲面进去,就肯定有多少根磁感线从曲面出来。因为如果有一根磁感线只进不出,那它就不可能是闭合的了,反之亦然。这就意味着进去的磁通量跟出来的磁通量相等,那么最后这个闭合曲面包含的总磁通量就恒为0了。这就是麦克斯韦方程组的第二个方程——高斯磁场定律的核心思想:闭合曲面包含的磁通量恒为0。
对比一下高斯电场定律和高斯磁场定律,我们会发现他们不仅是名字想象,思想也几乎是一模一样的,只不过目前还没有发现磁荷、磁单极子,所以高斯磁场定律的右边就是一个0。
金属棒要是顺着磁感线的方向运动就没有电流,但要是做切割磁感线的运动就能产生电流。如果改变一下磁场的强度,让磁场变强或者变弱一些,即便金属棒不动也会产生电流。法拉第仔细总结了这些情况,他发现不管是金属棒运动切割磁感线产生电流,还是磁场强度变化产生电流,都可以用一个通用的方式来表达:只要闭合回路的磁通量发生了改变,就会产生电流。磁通量是磁场强度B和面积a的乘积(B·a),切割磁感线其实是相当于改变了磁感线通过回路的面积a,改变磁场强度就是改变了B。不管是改变了a还是B,它们的乘积B·a(磁通量)肯定都是要改变的。 也就是说:只要通过曲面(我们可以把闭合回路当作一个曲面)的磁通量发生了改变,回路中就会产生电流,而且磁通量变化得越快,这个电流就越大。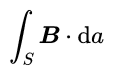
这里的曲面并不是闭合曲面,因此积分符号(拉长的S)中间没有一个圆圈。最终决定电流大小的并不是通过曲面的磁通量的大小,而是磁通量变化的快慢。我们衡量一个量变化快慢的方法是:给定一个变化的时间dt,看看这个量的变化dy是多少,如果这个量的变化很大我们就说它变化得很快,反之则变化得慢。因此,我们可以用这个量的变化dy和给定的时间dt的比值dy/dt来衡量量这个量y变化的快慢。所以,我们现在要衡量磁通量变化的快慢,那就只需要把磁通量的表达式替换掉上面的y就行了,那么通过曲面S的磁通量变化的快慢就可以这样表示:
一个曲面的磁通量发生了变化,它就会在这个曲面的边界感生出一个电场,然后这个电场会驱动导体中的自由电子定向移动,从而形成电流。因此,就算没有导线没有电流,这个电场依然存在。所以,需要描述的是被感生出来的电场。首先,一个曲面的磁通量发生了改变,就会在在曲面的边界感应出一个电场,这个电场是环绕着磁感线的,就像是磁感线的腰部套了一个呼啦圈。而且,你这个磁通量是增大还是减小,决定了这个电场是顺时针环绕还是逆时针环绕,如下图: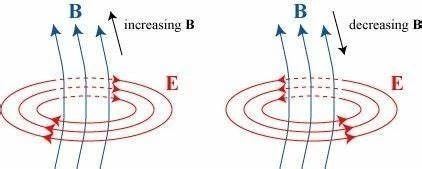
如果我们从上往下看的话,这个成闭环的感生电场就是如下图所示:它在这个闭环每点的方向都不一样,这样就刚好可以沿着回路驱动带电粒子,好像是电场在推着带电粒子在这里环里流动一样。
这里,就要引入一个新的概念:电场环流,电场的环流就是电场沿着闭合路径的线积分。这里有两个关键词:闭合路径和线积分。这个电场在大范围内(比如上面的整个圆环)方向是不一样的,但是,如果在圆环里取一个非常小的段dl,电场E就可以看做是一个恒定的了,这时候E·dl就是有意义的了。然后把这个环上所有部分的E·dl都累加起来,这就是对电场求线积分。而这个线积分就是电场环流,用符号表示就是这样:
积分符号下面的C表示这是针对曲线进行积分,积分符号中间的那个圆圈就表示这个是闭合曲线(电场形成的圆环)。电场环流的物理意义就是电动势,也就是电场对沿着这条路径移动的单位电荷所做的功。而用这个概念来描述变化的磁产生的电是更加合适的,它既包含了感生电场的大小信息,也包含了方向信息。麦克斯韦方程组的第三个方程——法拉第定律的最后表述就是这样的:曲面的磁通量变化率等于感生电场的环流。用公式表述就是这样:
为了维持一个系统的稳定,原来的磁通量是增加的,则感生电场产生的磁通量就必然要让原来的磁通量减小,反之亦然。这就是楞次定律。因此,磁通量的变化率前面会有个负号。导体运动导致的磁通量变化和磁场变化导致的磁通量变化。这两种情况其实是不一样的,但是它们居然又可以用一个统一的公式来表达,这其实是非常不自然的,当时的人们也只是觉得这是一种巧合罢了,但是爱因斯坦却不认为这是一种巧合,而是大自然在向我们暗示什么,他最终从这里发现了狭义相对论。也因为这两种情况不一样,所以,法拉第定律还有另外一个版本:它把这两种情况做了一个区分,认为只有磁场变化导致的磁通量变化才是法拉第定律,前面导体运动导致的磁通量变化只是通量法则。所以有时候就会看到法拉第定律的另一个版本:
对比一下这两个法拉第定律,我们发现后面这个只是把那个变化率从原来的针对整个磁通量移到了只针对磁场强度B(因为B不是只跟时间t有关,还可以跟其它的量有关,所以这里必须使用对时间的偏导的符号∂B/∂t),也就是说它只考虑变化磁场导致的磁通量变化。这种形式跟法拉第定律的微分形式对应得更好。奥斯特首先爆炸性地发现了电流的磁效应,发现了原来电和磁之间并不是毫无关系的。
如上图,假设电流从下往上,那么它在周围就会产生这样一个环形的磁场。磁场的方向可以用所谓的右手定则直观的判断:手握着导线,拇指指向电流的方向,那么你右手四指弯曲的方向就是磁场B的方向。 
安培环路定理的左边跟法拉第定律的左边很相似,因为法拉第定律说磁通量的变化会在它周围产生一个旋转闭合的电场,而电流的磁效应也是在电流的周围产生一个旋转闭合的磁场。电场环流(也就是电场在闭合路径的线积分)来描述这个旋转闭合的电场,那磁场环流(磁场在闭合路径的线积分)来描述这种旋转闭合的磁场。安培环路定理的右边,μ0是个常数(真空磁导率),I通常是用来表示电流的,enc这个右标是包含的意思。所以,右边这个带enc的电流I就表示被包含在闭合路径里的总电流,闭合路径就是左边积分符号中间那个圈圈表示的闭合路径。安培环路定理:通电导线周围会产生旋转磁场,可以在这个电流周围画一个圈,那么这个磁场的环流(沿着这个圈的线积分)就等于这个圈里包含的电流总量乘以真空磁导率。安培环路定理,虽然它确实描述了电生磁,但是它这里的电仅仅是电流(定理右边只有电流一项)。麦克斯韦认为“变化的电通量也能产生磁”,在他的概念模型里发现必须加入这样一项。而且,只有加上了这样一项,修正之后的安培环路定理才能跟高斯电场定律、高斯磁场定律、法拉第定律融洽相处,否则他们之间会产生矛盾。所以添加了这一项的就是麦克斯韦方程组的第四个方程——安培-麦克斯韦定律:
把它和安培环路定理对比一下,你就会发现它只是在在右边加了变化的电通量这一项,其它的都原封未动。E·a是电通量,套个面积分符号就表示通过曲面S的电通量,再加个d/dt就表示通过曲面S电通量变化的快慢。 ε0是真空中的介电常数,把这个常数和电通量变化的快慢乘起来就会得到一个跟电流的单位相同的量,它就被称为位移电流,如下图:
所以,我们经常能够听到别人说麦克斯韦提出了位移电流假说。其实,它的核心就是添加了“变化的电通量也能产生磁场”这一项,因为当时并没有实验能证明这一点,所以只能暂时称之为假说。在安培环路定理里添加了这一项之后,新生的安培-麦克斯韦定律就能跟其他的几条定律和谐相处了。而麦克斯韦之所以能够从他的方程组里预言电磁波的存在,这最后添加这项“变化的电通量产生磁场”至关重要。预言电磁波的关键就是“变化的电场产生磁场,变化的磁场产生电场”,这样变化的磁场和电场就能相互感生传向远方,从而形成电磁波。至此,麦克斯韦方程组的四个方程:描述静电的高斯电场定律、描述静磁的高斯磁场定律、描述磁生电的法拉第定律和描述电生磁的安培-麦克斯韦定律的积分形式就都说完了。把它们都写下来就是这样:
高斯电场定律说穿过闭合曲面的电通量正比于这个曲面包含的电荷量。法拉第定律说穿过曲面的磁通量的变化率等于感生电场的环流。安培-麦克斯韦定律说穿过曲面的电通量的变化率和曲面包含的电流等于感生磁场的环流。如果一个曲面是闭合的,那么通过它的通量就是曲面里面某种东西的量度。因为自然界存在独立的电荷,所以高斯电场定律的右边就是电荷量的大小,因为我们还没有发现磁单极子,所以高斯磁场定律右边就是0。如果一个曲面不是闭合的,那么它就无法包住什么,就不能成为某种荷的量度。但是,一个曲面如果不是闭合的,它就有边界,于是我们就可以看到这个非闭合曲面的通量变化会在它的边界感生出某种旋涡状的场,这种场可以用环流来描述。因而,我们就看到了:如果这个非闭合曲面的磁通量改变了,就会在这个曲面的边界感生出电场,这就是法拉第定律;如果这个非闭合曲面的电通量改变了,就会在这个曲面的边界感生出磁场,这就是安培-麦克斯韦定律的内容。当我们用闭合曲面和非闭合曲面的通量把这四个方程串起来的时候,你会发现麦克斯韦方程组还是很有头绪的,并不是那么杂乱无章。本文是长尾科技《最美的公式:你也能懂的麦克斯韦方程组(积分篇)》的学习总结,原文可以在长尾科技公众号查看。 | 