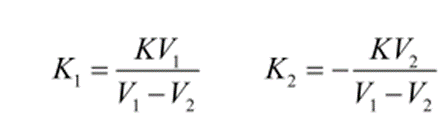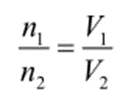› 首页 ›资讯 › 查看内容

Zemax光学设计实例（159）---双片式透镜的Seidel像差及校正

2022-5-9 21:41| 发布者：Davis| 查看：3705| 评论：0|原作者: 小小光08

摘要：This article discusses the Seidel aberrations and their correction in doublet lenses, particularly in Fraunhofer doublets. It explains the limitations of correcting Petzval curvature and the potential for optimizing the lens through glass selection and va

双片式物镜适用于很多小口径（最大为f/4）和小视场角的情况。

双片物镜的两个元件可以胶合在一起，也可以用空气间隔分开。在大多数情况下，两片透镜是胶合在一起的，因为这样公差更容易满足而且更牢固。

双片镜可以单独使用，也可以用作准直镜或者望远镜的物镜。许多透镜系统都含有若干个双片镜。

对单个双片式物镜探讨得到的大部分结果，也适用于复杂系统中的双片镜。

1. 双片式物镜的Seidel分析

1.1 色差

由在光阑处的薄透镜的轴向色差的Seidel方程：

若要使双片式物镜的轴向色差得以校正，需要满足的条件为：

同时，两个透镜的光焦度的和等于总光焦度：

联立上面两式可以求出：

在常规的光学设计中，常用玻璃库中，折射率范围在1.5至1.8之间，V值范围在90至20之间

例如，取V₁=60，V₂=36，代入上式可得：

1.2 像散与场曲的横向光线像差

三阶像散与场曲的横向光线像差为：

注意，δη`表示y分量（即y-z平面或子午面内的光线，），δξ`表示x分量（即x-z平面或弧矢面内的光线）。

又因为薄透镜在光阑上，

当n=1.5时，

则上式可以简化为：

例如，一个双片式透镜，焦距f`=100mm，即光焦度K=0.01mm^-1，孔径为f/5，透镜的数值孔径（在空气中）u`=n`sinU`约为0.1，半视场角为1°，那么像高η`=f`tam(1°)≈1.74mm。

因此，可以计算得到：

在ZEMAX中模拟上述这个例子。

在MFE中可以使用操作数查看透镜的数值孔径（在空气中）u`=n`sinU`约为0.1，和像高η`：

再查看Seidel Coefficient：

1.3 同时校正 Petzval 和与轴向色差

同时校正镜头的所有像差是不可能的。

对于可见光波段的双片式透镜，这点更为明显。双片式透镜可以改变的设计参数非常少，而且很多可以产生更好结果的玻璃不能用。

例如，两个贴在一起的双片式透镜的场曲为：

其轴向色差为：

这两个方程非常类似，若我们可以找到一对玻璃满足以下条件：

就可以同时校正S₄和C₁。

但是，在常用玻璃库中，可以看出至少在可见光波段，不存在这样的玻璃对。

因此，对于可见光波段的双片式，可以把 Petzval 和视为一个无法校正的像差。然而，在其他波段，也许会找到合适的玻璃对。

1.4 双片式透镜校正像差的可能性

由以上的分析，可以总结下双片式透镜校正像差的可能性，如下图：

2. 双胶合透镜

假设双胶合透镜的两个玻璃已选定。一旦确定这个双胶合物镜的光焦度，那么这个双胶合物镜只有曲率半径是可用变量。

注意：由于薄透镜理论对于双胶合透镜大体上是成立的，所以厚度对双胶合透镜的像差影响不大，若想要得到大的变化，则厚度需要改变很大。因此，对于双胶合透镜，厚度不是一个很有用的变量。

若这个透镜在光阑处，则彗差是透镜形状的线性函数，而球差则是透镜形状的二次函

数。因此总可以找到一个可以校正彗差的透镜形状，而球差的校正则需要找到一个合适的玻璃。

如下图所示，对应于特定火石玻璃，等晕（球差和彗差都被校正）消色差双胶合透镜所需要的冕牌玻璃。当满足彗差被校正时，在这条曲线以上的冕牌玻璃将得到正球差，曲线以下的冕牌玻璃将得到负球差。曲线的左端表示单片光焦度低的双胶合，即表面曲率比较小。当冕牌玻璃的选择接近火石玻璃（图的右上端），单片的光焦度增加，表面曲率增加，直到曲率大到不能制造。

双胶合的负元件起到两个作用，即引入负球差和负轴向色差。

可以证明，一对光焦度为+2.5和-1.5的双片透镜通常是校正球差且保持合理曲率的最优解。

2.1 双胶合透镜的优化

如果玻璃的选择合理，我们可以利用三个半径来优化透镜。

对于第一个元件是冕牌玻璃的双胶合透镜，即“冕牌在前双胶合”，可以从合适光焦度的等凸正元件开始，然后根据总光焦度的要求，计算出火石玻璃元件的光焦度。

若玻璃的选择不合理，那么使其中一个玻璃可变。设计者可以手动替换玻璃，也可以让程序自动替换。

若把玻璃设为变量，那么大多数的程序把玻璃的折射率和色散视为连续变量，最后让设计者在玻璃库中找最接近的实际玻璃。

2.2 冕牌在前的双胶合透镜实例

冕牌在前的双胶合，通常称为 Fraunhofer 双胶合。

在系统通用对话框中设置孔径。

在孔径类型中选择“Entrance PupilDiameter”，并根据设计要求输入“20”；

在视场设定对话框中设置2个视场，要选择“Angle”，如下图：

在波长设定对话框中，设置F,d.C(Visible)，如下图：

LDE参数，如下图：

查看2D Layout：

查看Ray Fan：

在Ray Fan中，可以看出一些信息：

轴上物点的像差曲线在某种程度上比标准的S形球差曲线更平，说明了其含有一点高级球差作为补偿。
球差的色变量即“色球差”，其原因是不同波长的像差曲线不相同。
短波与长波之间的距离比与中间波长之间的距离小，其告诉我们存在一些二级光谱。这一点表明，两端波长之间的色差校正并不与中间波长重合。
对比1度子午和弧矢像差曲线在原点的斜率，只看到一点点的像散。
轴上点和1度子午像差曲线在原点的斜率不一样，说明存在一些场曲，对于单正透镜这是必然的。

查看离焦点列图：

离焦点列图提供了轴上点和1度半视场的光线交点信息，这些交点处在近轴像面以及其他四个离焦面上，离焦间隔为0.05mm。当你对比轴上图（0 度）和离轴图（1 度），你可以看到像散效应导致的被拉长的点列图。

在点扩散图中，三种波长（d，C 和 F）的点叠加在一起，所以很难分辨出单个波长的点扩散图长什么样。

图中的彗差很小，即在横向光线像差曲线中具有二次曲线的形式，在离轴点扩散图中是“彗星”形状。

假设图中最大的横向光线像差是0.005mm，则可以推断边缘视场的光斑的总尺寸是这个的两倍即0.01mm。这表明在这个数倒数的频率处，即100线对/mm，离轴 MTF 值降到非常小。

查看几何MTF，在1度处的子午 MTF 曲线与这个预测一致。

以上表明，至少对于小孔径小视场的简单系统，Seidel 理论可以很好的预测实际镜头的像差。但是，对于大口径大视场的镜头，如照相物镜，高级像差就更重要了。

2.3 火石在前的双胶合透镜实例

火石元件在前的双胶合，也称为 Steinheil双胶合。

这两种形式的双胶合透镜的像差区别不大，但是Fraunhofer 形式在胶合面处的曲率更小，所以更佳。在制造透镜时，更小的曲率即更大的半径，可以同时抛光的透镜数更多，即更多经济效益。

在系统通用对话框中设置孔径。

在孔径类型中选择“Entrance PupilDiameter”，并根据设计要求输入“20”；

在视场设定对话框中设置2个视场，要选择“Angle”，如下图：

在波长设定对话框中，设置F,d.C(Visible)，如下图：

LDE参数，如下图：

查看2D Layout：

查看Ray Fan：

查看离焦点列图：

查看几何MTF：

对比Ray Fan，点列图和MTF曲线，可以看出冕牌在前的双胶合与火石在前的双胶合性能类似。

3. 分离双片式透镜

如果两个中间面没有胶合在一起，那么两个半径自然可以不相同，即额外增加了一个可用的变量。因此，这两个表面都可以用于控制球差和彗差。同样，选择玻璃的自由度也更大。

对于这种情况，使用薄透镜的球差和彗差方程，可以找到解析解。解析方法有一个好处，就是可以找到所有的可能解。

对于冕牌在火石玻璃前面的情况，我们可以找到两个解。其中一个对应于它的胶合形式即 Fraunhofer 双胶合透镜。而另一个双片式的火石元件的两个面都向前凸，即Gauss 双片式。可以看出第二个解的曲率更大，而通常更大的曲率意味着更大的高级像差。如下图所示：

分离双片式的优化通常比较简单，因为它有四个半径变量，通常能够满足四个条件。有时，中间的空气厚度也可以作为变量，这有助于减小高级球差和色球差。

3.1 分离的 Fraunhofer 双片式透镜实例

在系统通用对话框中设置孔径。

在孔径类型中选择“Entrance PupilDiameter”，并根据设计要求输入“20”；

在视场设定对话框中设置2个视场，要选择“Angle”，如下图：

在波长设定对话框中，设置F,d.C(Visible)，如下图：

LDE参数，如下图：

查看2D Layout：

查看Ray Fan：

查看离焦点列图：

查看几何MTF：

与胶合的情况相比，分离双片式的Ray Fan像差曲线更平，点列图更紧凑而且更对称。

分离式透镜的像差与胶合情况的像差非常相似，但是高级球差更小，色球差也减小了一点。高级球差被减小，是因为负透镜作用在正透镜所产生的具有像差的光束上。空气间隔的作用是改变光线在负透镜上的高度，以使负透镜的波前差被消除。和“固有像差”相比，这是一个“引入像差”的例子。

3.2 分离的 Gauss双片式透镜实例

在系统通用对话框中设置孔径。

在孔径类型中选择“Entrance PupilDiameter”，并根据设计要求输入“20”；

在视场设定对话框中设置2个视场，要选择“Angle”，如下图：

在波长设定对话框中，设置F,d.C(Visible)，如下图：

LDE参数，如下图：

查看2D Layout：

查看Ray Fan：

查看离焦点列图：

查看几何MTF：

由S₂的值可知，在1度视场，子午光线像差具有很强的U形曲线，其点列图也具有彗星形状；显然，即使视场角很小，彗差还是相当大。这个比较难校正，而且离轴 MTF 大大降低。因此，Gauss双片式比 Fraunhofer双片式差。

假设你在光学设计程序中任意输入分离双片式的曲率值，对像差指定权重，把所有的半径都设为变量，使用“局域梯度”优化方法，然后点击优化。你将得到 Fraunhofer 与 Gauss两种形式中的一个解，至于得到哪一个解，主要与你最初设置的曲率值有关。

上面的分析表明，虽然 Gauss 形式是一个好设计，但是 Fraunhofer 形式更好。若初始透镜与 Gauss 双片式类似，那么结果将是 Gauss，再怎么优化也无法使第二个元件弯向 Fraunhofer 解。其原因是，优化程序在做一个优化之前，只在变量空间中的一个“小步”进行探索。一旦找到了一个局域最小像差，那么要找到更好的局域最小值，它必须经过一段更差的像差即更大的评价函数。

对于分离的双片式，Gauss 解是“局域最小值”的一个典型例子。显然，对于这个例子，是由简单的薄透镜理论推断出其存在两个解。然而，对于更多元件的镜头，基于经验或直觉的传统方法，在某种程度上被所谓的“全局”优化方法替代。

4. 双片式透镜的局限性

除了像散和场曲，双片式物镜还存在二级光谱和五级球差。因为与五级球差相关的波前差与光瞳的六次方成正比，所以大孔径的镜头受五级球差的影响。

此外，小孔径宽波段的镜头可能会受二级光谱的限制，特别是对于大焦距的系统更严重，除非使用了反常玻璃。

我们已经知道，分离双片式更好设计，因为它相对于胶合双片式多了一个变量。而且，分离双片式的性能更好，因为空气间隔变量可以用于校正或者减少五级球差。然而，就制造而言，双胶合更好，因为胶合面的像差远小于双分离中的空气玻璃界面的像差。这意味着双胶合的制造公差更宽松。而且，双胶合透镜显然比分离式更耐用更容易调试；分离式的中间空气厚度往往是一个非常敏感的设计参数，在振动和撞击的情况下还容易偏心。